Abstände und Winkel
Neben der (besonderen) gegenseitigen Lage von Geraden und Ebenen, geht es in der Analytischen Geometrie auch um die Berechnung von Abst?nden und Winkel zwischen Punkten, Geraden und Ebenen. Die meisten dieser Berechnungsmethoden beruhen auf die geschickte Verkn?pfung von Methoden, die du schon in fr?heren Kapiteln kennengelernt hast. Genauso ist dies mit Spiegelungsaufgaben, bei denen Objekte an einem Punkt, einer Gerade oder einer Ebene gespiegel werden sollen. Diese Aufgaben sind sehr beliebt (zumindest bei den Lehrern), weil der L?sungsansatz oft aus der logischen Aneinanderreihung von Methoden besteht, die du von den Grundlagen der Geraden- und Ebenenkonstruktion und den einfachen Vektorrechnung schon kennst.Abstand Punkt-Punkt
Abstand Punkt - Gerade


m13v0009 In diesem Lektionsvideo wird die Methode des "laufenden Punktes" zur Bestimmung des Abstands eines Punktes von einer Geraden vorgestellt. Dazu wird aus der Schar der Verbindungsvektoren vom gegebenen Punkt zu Punkten auf der Geraden derjenige bestimmt, der senkrecht zur Geraden steht. Der Betrag dieses Vektors ergibt den gesuchten Abstand. Arbeitsblatt zum Download | auf teilen
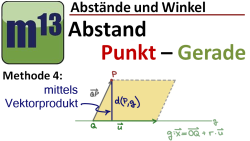

m13v0406 In diesem Video wird eine weitere Methode vorgestellt, mit der man den Abstand eines Punktes von einer Geraden bestimmen kann - diesmal mit Hilfe des Vektorprodukts (Kreuzproduktes). Anders als bei anderen Methoden, wird der Abstand direkt, d.h. ohne über den Umweg der Lotfußpunktbestimmung, berechnet. Also immer, wenn man den Lotfußpunkt nicht explizit berechnen muss, ist dies eine sehr schnelle Berechnungsmethode des Abstandes Punkt-Gerade. | auf teilen
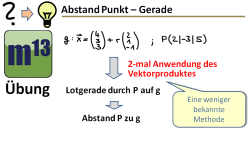

m13v0631 In diesem Video wird eine andere Methode der Abstandsbestimmung Punkt-Gerade gezeigt, bei der zweimal das Vektorprodukt zum Einsatz kommt. Man beginnt mit der Betrachtung, dass Gerade und Punkt in einer gemeinsamen Ebene liegen, dann sucht man zunächst einen Normalenvektor und dann einen Vektor, der zum Normalenvektor und der Geraden senkrecht ist - dies ist die Richtung der Lotgeraden. Der Rest ist dann Routine... Arbeitsblatt zum Download | auf teilen
Abstand Punkt - Ebene


m13v0159 In diesem Video wird erklärt, wie man den Abstand eines Punktes von der Ebene bestimmt - in diesem Fall mit Hilfe einer Lotgeraden. | auf teilen
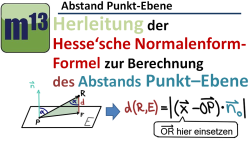

m13v0464 In diesem Video wird die Formel zur Berechnung des Abstandes Punkt-Ebene über die Hessesche Normalenform hergeleitet. | auf teilen


m13v0775 Wenn die Ebenengleichung in der Hesse'schen Normalenform vorliegt, kann man damit sehr einfach den Abstand eines Punktes von der Ebene bestimmen. Besonders einfach ist es, wenn der Punkt der Koordinatenursprung ist. So ein Fall wird in dieser Übungsaufgabe behandelt. Arbeitsblatt zum Download | auf teilen
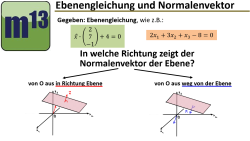

m13v0701 Aus der Ebenengleichung kann man einen Normalenvektor der Ebene ermitteln; aber dieser Normalenvektor kann ja in zwei verschiedene Richtungen zeigen. Wie kann man feststellen, in welche Richtung der Normalenvektor zeigt, wenn man diesen am Koordinatenursprung ansetzt - zur Ebene hin, oder von der Ebene weg? In diesem Video wird gezeigt, wie man dies untersuchen kann... Arbeitsblatt zum Download | auf teilen

m13v0270 Dies ist ein Übungsvideo, in dem Punkte ermittelt werden sollen, die einen bestimmten Abstand zu einem Lotfußpunkt bzw. einer Ebene haben. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0323 In diesem Ãœungsvideo sollen die Punkte auf der x2-Achse bestimmt werden, die einen bestimmten Abstand zu einer gegebenen Ebene haben. Dies ist eine Aufgabe, so wie sie im hilfsmittelfreien Teil im Abitur drankam. Arbeitsblatt zum Download | auf teilen


m13v0725 Bei dieser klausurtypischen Aufgabe untersuchen wir das Zusammenspiel zwischen einer Geraden und einer Ebene. Die Gerade schneidet die Ebene. Nun geht es darum, Punkte auf der Geraden zu finden, die von der Ebene einen vorgegebenen (senkrechten) Abstand haben. Arbeitsblatt zum Download | auf teilen
Abstand Gerade - Gerade


m13v0011 In diesem Video wird erklärt, wie man den Abstand windschiefer Geraden bestimmt. Der kürzeste Abstand zweier windschiefer Geraden ist die Strecke, die gleichzeitig senkrecht auf beiden Geraden steht (das gemeinsame Lot). Hier wird erläutert, wie man dieses gemeinsame Lot ermittelt. Es gibt eine weitere Methode zur Bestimmung des Abstandes von winschiefen Geraden, die in einem separaten Video (folgt in Kürze) erläutert wird. | auf teilen


m13v0012 In diesem Video wird erklärt, wie man den Abstand windschiefer Geraden bestimmt - in diesem Fall mittels einer Hilfsebene. In einem anderen Video habe ich vorgemacht, wie man das über ein gemeinsames Lot beider Geraden machen kann | auf teilen


m13v0744 Wenn man zwei Geraden mit besonderer Lage im Raum gegeben hat (Parallelität zu Koordinatenachsen bzw. zu Koordinatenebenen), so ist es sehr einfach deren Abstand zu bestimmen. In diesem Video wird dies an drei Beispielen vorgemacht. Arbeitsblatt zum Download | auf teilen
Abstand Gerade - Ebene


m13v0847 Bei dieser Aufgabe hast du eine Geradenschar und eine Ebene gegeben. Du sollst prüfen, ob es Geraden aus der Schar gibt, die parallel zur Ebene verlaufen und einen festgelegten Abstand zu ihr haben. Arbeitsblatt zum Download | auf teilen
Abstand Ebene-Ebene

m13v0207 Zwei Ebenen sind in Parameter bzw. Normalenform gegeben. Zu zeigen ist, dass die Ebenen parallel sind, und man soll ihren Abstand bestimmen. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0489 Ein weiteres Video aus der Serie "So ähnlich im Abi gesehen". Eine Ebene E ist gegeben. Gesucht sind die zu E parallelen Ebenen, welche vom Koordinatenursprung den Abstand 5 haben. Eine ähnliche Aufgabe wurde im Abi des Landes Baden-Württemberg im Jahr 2016 gestellt. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0697 Ein Video zu Abständen paralleler Ebenen: Zu einer gegebenen Ebene gibt es zwei Ebenen, die denselben Abstand zu dieser haben. Bei dieser Aufgabe sollen die Gleichungen solcher Ebenen bestimmt werden. Arbeitsblatt zum Download | auf teilen

