Lineare Gleichungssysteme II (drei und mehr Variablen)
Das Gauß-Verfahren zum Lösen Linearer Gleichungssysteme
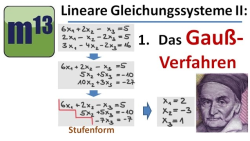
LGS: (1.) Lineare Gleichungssysteme mit Gauß-Verfahren lösen
m13v0232 In diesem Video lernst du, wie man ein lineares Gleichungssystem (LGS) mit Hilfe des Gauß-Verfahrens löst.
Hierbei lernst du im einzelnen:
- welche Rechenoperationen beim Lösen von linearen Gleichungssystemen erlaubt sind
- wie man ein LGS schrittweise auf die Stufenform (Dreiecksform) bringt
- wie man ein auf die Stufenform gebrachtes LGS rückwärts/von unten nach oben löst
| auf teilen
m13v0232 In diesem Video lernst du, wie man ein lineares Gleichungssystem (LGS) mit Hilfe des Gauß-Verfahrens löst.
Hierbei lernst du im einzelnen:
- welche Rechenoperationen beim Lösen von linearen Gleichungssystemen erlaubt sind
- wie man ein LGS schrittweise auf die Stufenform (Dreiecksform) bringt
- wie man ein auf die Stufenform gebrachtes LGS rückwärts/von unten nach oben löst
| auf teilen

LGS: (2.) LGS übersichtlich Lösen mit erweiterter Koeffizientenmatrix
m13v0233 In diesem Video lernst eine Schreibweise kennen, mit der man lineare Gleichungssysteme (LGS) übersichtlich und schnell lösen kann - die erweiterte Koeffizientenmatrix.
Die Schreibweise der erweiterten Koeffizientenmatrix ist nicht nur vorteilhaft beim "von Hand"-Lösen von LGS, sondern sie wird auch für die Eingabe von LGS in den Taschenrechner verwendet.
| auf teilen
m13v0233 In diesem Video lernst eine Schreibweise kennen, mit der man lineare Gleichungssysteme (LGS) übersichtlich und schnell lösen kann - die erweiterte Koeffizientenmatrix.
Die Schreibweise der erweiterten Koeffizientenmatrix ist nicht nur vorteilhaft beim "von Hand"-Lösen von LGS, sondern sie wird auch für die Eingabe von LGS in den Taschenrechner verwendet.
| auf teilen
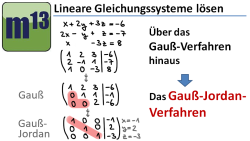
Gauß-Jordan-Verfahren zum Lösen von Linearen Gleichungssystemen
m13v0479 In diesem Video wird ein Algorithmus zum Lösen von Linearen Gleichungssystemen vorgestellt, der im Prinzip wie der Gauß-Algorithmus funktioniert, aber so lange durchlaufen wird, bis die Koeffizientenmatrix am Ende nur noch Einsen auf der Hauptdiagonale enthält. Dies ist das sogenannte Gauß-Jordan-Verfahren ? eine Methode, die man kennen sollte, weil sie z.B. der manuellen Berechnung von Inversen Matrizen benötigt wird. | auf teilen
m13v0479 In diesem Video wird ein Algorithmus zum Lösen von Linearen Gleichungssystemen vorgestellt, der im Prinzip wie der Gauß-Algorithmus funktioniert, aber so lange durchlaufen wird, bis die Koeffizientenmatrix am Ende nur noch Einsen auf der Hauptdiagonale enthält. Dies ist das sogenannte Gauß-Jordan-Verfahren ? eine Methode, die man kennen sollte, weil sie z.B. der manuellen Berechnung von Inversen Matrizen benötigt wird. | auf teilen
Welche Lösungsmengen gibt es bei Linearen Gleichungssystemen?
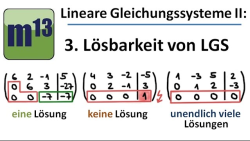
LGS: (3.) Lösungsmenge Linearer Gleichungssysteme - eine Lösung, keine Lösung, unendlich viele Lösungen
m13v0234 Nachdem man das LGS mit dem Gauß-Verfahren auf die Stufenform gebracht hat, kann man an der letzten Zeile des LGS erkennen, welche Art von Lösungsmenge (eine Lösung, keine Lösung, unendlich viele Lösungen) das LGS hat. Das Video zeigt, wie es geht... | auf teilen
m13v0234 Nachdem man das LGS mit dem Gauß-Verfahren auf die Stufenform gebracht hat, kann man an der letzten Zeile des LGS erkennen, welche Art von Lösungsmenge (eine Lösung, keine Lösung, unendlich viele Lösungen) das LGS hat. Das Video zeigt, wie es geht... | auf teilen
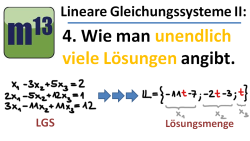
LGS: (4.) Lösungsmenge bei unendlich vielen Lösungen angeben
m13v0251 In diesem Video lernst du, wie man bei einem linearen Gleichungssystem, das unendlich viele Lösungen hat, die Lösungsmenge angeben kann.
| auf teilen
m13v0251 In diesem Video lernst du, wie man bei einem linearen Gleichungssystem, das unendlich viele Lösungen hat, die Lösungsmenge angeben kann.
| auf teilen
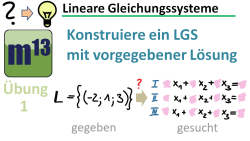
Lineares Gleichungssystem (LGS) mit vorgegebener Lösungsmenge aufstellen
m13v0411 In diesem Übungsvideo sollst du ein Lineares Gleichungssystem (LGS) konstruieren, welches eine vorgegebene Lösungsmenge hat. Im Video wird die "Gauß-Verfahren-Rückwärts"-Methode verwendet. | auf teilen
Arbeitsblatt zum Download
m13v0411 In diesem Übungsvideo sollst du ein Lineares Gleichungssystem (LGS) konstruieren, welches eine vorgegebene Lösungsmenge hat. Im Video wird die "Gauß-Verfahren-Rückwärts"-Methode verwendet. | auf teilen
Arbeitsblatt zum Download

LGS mit Lösung (0,0,0) oder keiner Lösung konstruieren
m13v0412 Ein weiteres Übungsvideo, bei dem du Lineare Gleichungssysteme konstruieren sollst, die eine vorgegebene Lösungsmenge haben. Diesmal soll ein LGS aufgestellt werden, welches die Lösungsmenge (0,0,0) hat und eines, das keine Lösung hat. | auf teilen
Arbeitsblatt zum Download
m13v0412 Ein weiteres Übungsvideo, bei dem du Lineare Gleichungssysteme konstruieren sollst, die eine vorgegebene Lösungsmenge haben. Diesmal soll ein LGS aufgestellt werden, welches die Lösungsmenge (0,0,0) hat und eines, das keine Lösung hat. | auf teilen
Arbeitsblatt zum Download

Lineares Gleichungssystem mit vorgegebener Lösungsmenge in Matrixschreibweise konstruieren
m13v0714 Diese Übungsaufgabe behandelt die Lösungsmenge eines linearen Gleichungssystems in Matrixform. Du sollst eine 3×2-Koeffizientenmatrix A erstellen und zwei Ergebnisvektoren entwerfen, um einmal eine eindeutige Lösung und einmal keine Lösung zu erhalten. Die Besonderheit dieser Aufgabe besteht darin, dass das lineare Gleichungssystem mehr Gleichungen als Unbekannte hat. Dieses Video ist eine nützliche Ressource für alle, die ihre Kenntnisse zu linearen Gleichungssystemen und deren Lösungsmengen erweitern möchten. | auf teilen
Arbeitsblatt zum Download
m13v0714 Diese Übungsaufgabe behandelt die Lösungsmenge eines linearen Gleichungssystems in Matrixform. Du sollst eine 3×2-Koeffizientenmatrix A erstellen und zwei Ergebnisvektoren entwerfen, um einmal eine eindeutige Lösung und einmal keine Lösung zu erhalten. Die Besonderheit dieser Aufgabe besteht darin, dass das lineare Gleichungssystem mehr Gleichungen als Unbekannte hat. Dieses Video ist eine nützliche Ressource für alle, die ihre Kenntnisse zu linearen Gleichungssystemen und deren Lösungsmengen erweitern möchten. | auf teilen
Arbeitsblatt zum Download

Lineares Gleichungssystem lösen, das in Matrixfrom gegeben ist
m13v0797 Diese Aufgabe behandelt das Lösen linearer Gleichungssysteme, die in Form einer Matrix-Vektor-Gleichung gegeben sind. Du sollst den allgemeinen Lösungsvektor bestimmen, falls unendlich viele Lösungen existieren, und zusätzlich eine spezielle Lösung finden, indem der Wert einer Variable vorgegeben wird. Außerdem überprüfst du, ob das Gleichungssystem eindeutig lösbar ist oder keine Lösung hat. | auf teilen
Arbeitsblatt zum Download
m13v0797 Diese Aufgabe behandelt das Lösen linearer Gleichungssysteme, die in Form einer Matrix-Vektor-Gleichung gegeben sind. Du sollst den allgemeinen Lösungsvektor bestimmen, falls unendlich viele Lösungen existieren, und zusätzlich eine spezielle Lösung finden, indem der Wert einer Variable vorgegeben wird. Außerdem überprüfst du, ob das Gleichungssystem eindeutig lösbar ist oder keine Lösung hat. | auf teilen
Arbeitsblatt zum Download

LGS aufstellen zu gegebener, unendlich großer Lösungsmenge
m13v0560 Bei dieser Aufgabe sollst du ein LGS aufstellen, welches eine vorgegebene, unendlich große Lösungsmenge hat. Das LGS soll aus drei Zeilen bestehen, und jede der Variablen x1, x2 und x3 soll in jeder Zeile vorkommen. Die Richtigkeit des aufgestellten LGS soll anhand einer der unendlich vielen Lösung demonstriert werden. | auf teilen
Arbeitsblatt zum Download
m13v0560 Bei dieser Aufgabe sollst du ein LGS aufstellen, welches eine vorgegebene, unendlich große Lösungsmenge hat. Das LGS soll aus drei Zeilen bestehen, und jede der Variablen x1, x2 und x3 soll in jeder Zeile vorkommen. Die Richtigkeit des aufgestellten LGS soll anhand einer der unendlich vielen Lösung demonstriert werden. | auf teilen
Arbeitsblatt zum Download

Lineares Gleichungssystem: zwei Lösungen gegeben - finde alle!
m13v0749 Wenn man zwei Lösungen eines linearen Gleichungssystems kennt, dann weiß man, dass das LGS tatsächlich unendlich viele Lösungen hat. Hier sind zwei Lösungen vorgegeben, und du sollst die Menge aller Lösungen bestimmen und ein mögliches zugehöriges LGS aufstellen. Dies ist eine wichtige Aufgabe, mit der du dein Verständnis zu Linearen Gleichungssystemen überprüfen kannst. | auf teilen
Arbeitsblatt zum Download
m13v0749 Wenn man zwei Lösungen eines linearen Gleichungssystems kennt, dann weiß man, dass das LGS tatsächlich unendlich viele Lösungen hat. Hier sind zwei Lösungen vorgegeben, und du sollst die Menge aller Lösungen bestimmen und ein mögliches zugehöriges LGS aufstellen. Dies ist eine wichtige Aufgabe, mit der du dein Verständnis zu Linearen Gleichungssystemen überprüfen kannst. | auf teilen
Arbeitsblatt zum Download

Lineares Gleichungssystem (LGS) mit unendlich vielen Lösungen untersuchen
m13v0857 Bei dieser Aufgabe sollst du die unendlich große Lösungsmenge eines linearen Gleichungssystems mit drei Variablen in Form eines allgemeinen Lösungsvektors beschreiben. Darauf aufbauend sollst du gezielt einzelne Lösungen finden, die zusätzliche Bedingungen erfüllen. | auf teilen
Arbeitsblatt zum Download
m13v0857 Bei dieser Aufgabe sollst du die unendlich große Lösungsmenge eines linearen Gleichungssystems mit drei Variablen in Form eines allgemeinen Lösungsvektors beschreiben. Darauf aufbauend sollst du gezielt einzelne Lösungen finden, die zusätzliche Bedingungen erfüllen. | auf teilen
Arbeitsblatt zum Download

Verständnisaufgaben zu Linearen Gleichungssystemen und deren Lösungsmengen
m13v0748 Dies ist eine Übung zur Prüfung deines Verständnisses von linearen Gleichungssystemen. Deine Aufgabe ist es, Gleichungssysteme zu erstellen − mit entsprechender Begründung −, die entweder unendlich viele, genau eine oder keine Lösung haben. Die Herausforderung besteht darin, ausgehend von einem ursprünglichen Gleichungssystem dieses so zu modifizieren, dass sich unterschiedliche Lösungsmengen ergeben. Hierfür ist ein grundlegendes Verständnis darüber erforderlich, wie lineare Gleichungssysteme funktionieren. | auf teilen
Arbeitsblatt zum Download
m13v0748 Dies ist eine Übung zur Prüfung deines Verständnisses von linearen Gleichungssystemen. Deine Aufgabe ist es, Gleichungssysteme zu erstellen − mit entsprechender Begründung −, die entweder unendlich viele, genau eine oder keine Lösung haben. Die Herausforderung besteht darin, ausgehend von einem ursprünglichen Gleichungssystem dieses so zu modifizieren, dass sich unterschiedliche Lösungsmengen ergeben. Hierfür ist ein grundlegendes Verständnis darüber erforderlich, wie lineare Gleichungssysteme funktionieren. | auf teilen
Arbeitsblatt zum Download

Unendliche vielen Lösungen eines LGS - unterschiedliche Darstellungsmöglichkeit der Lösungsmenge
m13v0423 Zwei Schüler haben dasselbe LGS gelöst, dabei heraus bekommen, dass das LGS unendlich viele Lösungen hat. Beide haben eine jeweils eine Lösungsmenge, die allerdings unterschiedlich aussieht. Du sollst nun nachweisen, dass das beide Darstellungsmöglichkeiten für das gegebenen LGS richtig sind. | auf teilen
Arbeitsblatt zum Download
m13v0423 Zwei Schüler haben dasselbe LGS gelöst, dabei heraus bekommen, dass das LGS unendlich viele Lösungen hat. Beide haben eine jeweils eine Lösungsmenge, die allerdings unterschiedlich aussieht. Du sollst nun nachweisen, dass das beide Darstellungsmöglichkeiten für das gegebenen LGS richtig sind. | auf teilen
Arbeitsblatt zum Download
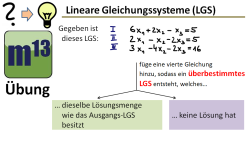
Überbestimmtes Lineares Gleichungssystem (LGS) und dessen Lösungsmenge | Übung
m13v0645 Bei dieser Aufgabe soll man ein gegebenes Lineare Gleichungssystem (LGS) mit drei Unbekannten und drei Gleichungen so erweitern, dass ein überbestimmtes LGS entsteht. Dabei soll einmal ein LGS mit der ursprünglichen Lösungsmenge, und einmal ein LGS mit leerer Lösungsmenge erzeugt werden. | auf teilen
Arbeitsblatt zum Download
m13v0645 Bei dieser Aufgabe soll man ein gegebenes Lineare Gleichungssystem (LGS) mit drei Unbekannten und drei Gleichungen so erweitern, dass ein überbestimmtes LGS entsteht. Dabei soll einmal ein LGS mit der ursprünglichen Lösungsmenge, und einmal ein LGS mit leerer Lösungsmenge erzeugt werden. | auf teilen
Arbeitsblatt zum Download
Die Lösungsmenge eines LGS kann man auch geometrisch interpretieren - zum Beispiel bei 3 Gleichungen mit 3 Unbekannten. Ich arbeite an einer Serie von Videos über die Lage dreier Ebenen. Wenn die Serie fertig ist, soll an dieser Stelle ein entsprechender Verweis zum Kapitel Ebenen II eingefügt werden.
Lineare Gleichungssysteme mit Parameter

Lineares Gleichungssystem (LGS) mit Parameter lösen (Übung 1)
m13v0265 In diesem Übungsvideo geht es um das Lösen eines Linearen Gleichungssystems (LGS), das neben den Variablen auf der Ergebnisseite auch einen Parameter r enthält. Es soll die Lösungsmenge in Abhängigkeit von r bestimmt werden.
| auf teilen
Arbeitsblatt zum Download
m13v0265 In diesem Übungsvideo geht es um das Lösen eines Linearen Gleichungssystems (LGS), das neben den Variablen auf der Ergebnisseite auch einen Parameter r enthält. Es soll die Lösungsmenge in Abhängigkeit von r bestimmt werden.
| auf teilen
Arbeitsblatt zum Download
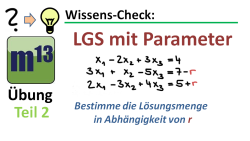
Lineares Gleichungssystem (LGS) mit Parameter lösen (Übung 2)
m13v0266 Dies ist das zweite Übungsvideo zum Lösen eines Linearen Gleichungssystems (LGS) mit Parameter. Hier wird sich ergeben, dass vom Parameter abhängt, ob das LGS unendlich viele Lösungen oder keine Lösung hat. | auf teilen
Arbeitsblatt zum Download
m13v0266 Dies ist das zweite Übungsvideo zum Lösen eines Linearen Gleichungssystems (LGS) mit Parameter. Hier wird sich ergeben, dass vom Parameter abhängt, ob das LGS unendlich viele Lösungen oder keine Lösung hat. | auf teilen
Arbeitsblatt zum Download
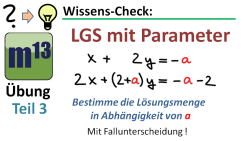
Lineares Gleichungssystem (LGS) mit Parameter lösen (Übung 3) - mit Fallunterscheidung
m13v0430 Ein drittes Übungsvideo zum Lösen eines Linearen Gleichungssystems (LGS) mit Parameter. Diese Aufgabe ist etwas schwieriger, denn hier muss man eine Fallunterscheidung machen. Auch hier hängt es vom Parameterwert ab, ob das LGS eine, keine oder unendlich viele Lösungen hat. | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon
m13v0430 Ein drittes Übungsvideo zum Lösen eines Linearen Gleichungssystems (LGS) mit Parameter. Diese Aufgabe ist etwas schwieriger, denn hier muss man eine Fallunterscheidung machen. Auch hier hängt es vom Parameterwert ab, ob das LGS eine, keine oder unendlich viele Lösungen hat. | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon

Lösungsmengen von Linearen Gleichungssystemen (Aufgabe so ähnlich im Abi gesehen)
m13v0480 Bei dieser Aufgabe sollst du untersuchen, welchen Einfluss ein Koeffizientenparameter auf die Lösungsmenge eines Linearen Gleichungssystems hat. Eine ähnliche Aufgabe wurde im hilfsmittelfreien Teil im Abitur des Landes NRW im Jahr 2017 gestellt. | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon
m13v0480 Bei dieser Aufgabe sollst du untersuchen, welchen Einfluss ein Koeffizientenparameter auf die Lösungsmenge eines Linearen Gleichungssystems hat. Eine ähnliche Aufgabe wurde im hilfsmittelfreien Teil im Abitur des Landes NRW im Jahr 2017 gestellt. | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon

LGS mit Parameter (mehrere Grundaufgaben)
m13v0781 In dieser Aufgabe testest du deine Fähigkeiten im Umgang mit linearen Gleichungssystemen (LGS) mit einem Parameter. Du löst das System für verschiedene Parameterwerte, untersuchst, wann keine Lösung existiert, und bestimmst die Lösungsmenge des LGS allgemein in Abhängigkeit vom Parameter. Zusätzlich ermittelst du den Parameterwert, bei dem eine vorgegebene Lösung des Systems erfüllt wird. | auf teilen
Arbeitsblatt zum Download
m13v0781 In dieser Aufgabe testest du deine Fähigkeiten im Umgang mit linearen Gleichungssystemen (LGS) mit einem Parameter. Du löst das System für verschiedene Parameterwerte, untersuchst, wann keine Lösung existiert, und bestimmst die Lösungsmenge des LGS allgemein in Abhängigkeit vom Parameter. Zusätzlich ermittelst du den Parameterwert, bei dem eine vorgegebene Lösung des Systems erfüllt wird. | auf teilen
Arbeitsblatt zum Download
In der Mittelstufe hattest du schon mit Linearen Gleichungssystemen zu tun. Diese hatten damals in der Regel nur zwei Unbekannte und wurden mit dem Einsetzungsverfahren, dem Gleichsetzungsverfahren oder dem Additionsverfahren gelöst.
Weil Lineare Gleichungssysteme wesentliche Werkzeuge der Linearen Algebra und der Analytischen Geometrie sind, kommen wir jetzt noch einmal auf diese zurück. Diesmal werden auch LGS mit mehr als zwei Unbekannten behandelt. Zunächst lernst du das Gauß-Verfahren (welches auf dem Additionsverfahren beruht) zum systematischen Lösen von LGS kennen, bei dem man das LGS Schritt für Schritt in die sogenannte Stufenform (oder Dreiecksform) überführt. Du wirst erfahren, wie man die Art der Lösungsmenge eines LGS nach Überführung in die Stufenform erkennt und wirst lernen, wie man die Lösungsmenge eines LGS angibt, das unendlich viele Lösungen hat.