Übergangsmatrizen

Übergangs- oder Austauschmatrizen treten in vielen Prozessen auf, bei denen Wahrscheinlichkeiten oder Anteile von einer Verteilung in die nächste überführt werden. Sie sind quadratische Matrizen, deren Spalten (oder Zeilen, je nach Konvention) Wahrscheinlichkeiten beschreiben.
In diesem Kapitel lernst du, wie man Übergangsmatrizen aufstellt, Verteilungen berechnet und stationäre Zustände findet.

Grundlagen und erste Aufgaben

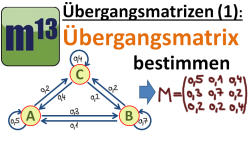
(1): Übergangsgraph und Übergangsmatrix aufstellen | Austauschprozesse
m13v0095 Übergangsgraph und Übergangsmatrix für Austauschprozesse aufstellen - so geht es.
Dieser Aufgabentyp ist oft der erste Teil einer Aufgabe über Übergangs- oder Austauschmatrizen.
| auf teilen

(2): nächste Verteilung(en) bestimmen
m13v0209 Wird eine Austausch-(Übergangsmatrix) auf einen Verteilungsvektor angewendet, erhält man die entsprechende, neue Verteilung. Das Bestimmen der nächsten Verteilung ist eine wichtige Grundaufgabe bei Übergangs- oder Austauschmatrizen.
| auf teilen

(3.) vorherige Verteilung berechnen mit LGS bzw. Inverser Matrix
m13v0210 Bei Austausch- und Übergangsprozessen, die vorherige Verteilung berechnen - hier erfährst du, wie es geht
Auch dieser Aufgabentyp ist eine Grundaufgabe bei Übergangs- oder Austauschmatrizen.
| auf teilen

Stationäre Zustände und Langzeitverhalten

(4.) stabile Verteilung, Fixvektor, Grenzverteilung bestimmen
m13v0212 Wie man die stationäre Verteilung (Grenzverteilung; Fixvektor) bei Austausch-Prozessen bestimmt. Schritt für Schritt erklärt.
| auf teilen

(5.) Grenzmatrix bestimmen
m13v0229 In diesem Video lernst du, wie man die Grenzmatrix einer Übergangsmatrix/Austauschmatrix bestimmt. Über die Grenzmatrix gelangt man von einer gegebenen Ausgangs- oder Zwischenverteilung direkt zur stabilen Verteilung.
Wenn man die stabile Verteilung kennt, kann man die Grenzmatrix berechnen.
| auf teilen

Besondere Aufgabentypen

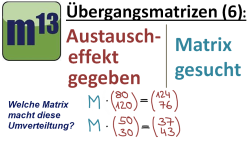
(6.) Austauscheffekt einer Matrix gegeben, zugrundeliegende Matrix gesucht
m13v0329 In diesem Video wird der Fall behandelt, dass man den Austauscheffekt einer Matrix kennt (d.h. man weiß wie eine gegebene Verteilung nach Anwendung der Matrix umverteilt wird), aber kann hat die zugrundeliegende Matrix nicht gegeben. Wie man die Matrix findet, wird hier gezeigt. | auf teilen

Stochastische Matrix und Zustandsvektor (Übungsaufgabe)
m13v0685 Beim Multiplizieren einer stochastischen Matrix mit einem Zustandsvektor ändert sich die Summe der Zustände nicht. Bei dieser Aufgabe sollst du zeigen, warum das so ist... | auf teilen
Arbeitsblatt zum Download

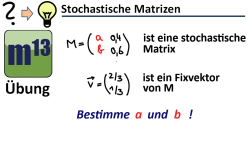
Fixvektor gegeben, stochastische Matrix gesucht (Übung)
m13v0474 Bei dieser Aufgabe hast du eine unvollständige stochastische Übergangsmatrix gegeben, aber du kennst einen Fixvektor dieser Matrix. Nun sollst du die fehlenden Matrixelemente bestimmen. | auf teilen
Arbeitsblatt zum Download

Austauschmatrix aus Verteilung und Folgeverteilung bestimmen
m13v0568 Gegeben ist eine Startverteilung sowie zwei Folgeverteilungen. Nun soll die zugrundeliegende Übergangsmatrix ermittelt werden, welche die Umverteilung zwischen den aufeinanderfolgenden Verteilungen bewirkt. | auf teilen
Arbeitsblatt zum Download