Einführung in den Funktionsbegriff
Hinweis
Grundverständnis von Funktionen
Stelle und Punkt einer Funktion - was ist der Unterschied?
m13v0271 In diesem kurzen Video wird erklärt, was der Unterschied zwischen einer Stelle und einem Punkt ist. Du wirst sehen, dass zum Beispiel die Wörter Extremstelle und Extrempunkt bzw. Wendestelle und Wendepunkt unterschiedliche Bedeutungen haben. | auf teilen
m13v0271 In diesem kurzen Video wird erklärt, was der Unterschied zwischen einer Stelle und einem Punkt ist. Du wirst sehen, dass zum Beispiel die Wörter Extremstelle und Extrempunkt bzw. Wendestelle und Wendepunkt unterschiedliche Bedeutungen haben. | auf teilen
Symmetrien von Funktionsgraphen
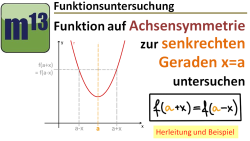
Allgemeine Symmetrie eines Funktionsgraphen zu einer senkrechten Geraden x=a nachweisen
m13v0549 In diesem Video wird die Gleichung hergeleitet, mit der man rechnerisch prüfen kann, ob der Graph einer Funktion achsensymmetrisch ist zu einer senkrechten Spiegelachse x=a. Die Anwendung wird an einem Beispiel vorgemacht. | auf teilen
m13v0549 In diesem Video wird die Gleichung hergeleitet, mit der man rechnerisch prüfen kann, ob der Graph einer Funktion achsensymmetrisch ist zu einer senkrechten Spiegelachse x=a. Die Anwendung wird an einem Beispiel vorgemacht. | auf teilen
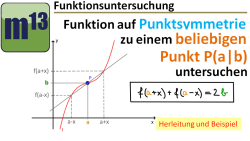
Allgemeine Symmetrie eines Funktionsgraphen zu einem Punkt P(a|b) nachweisen
m13v0544 In diesem Video wird die Gleichung hergeleitet, mit der man rechnerisch prüfen kann, ob der Graph einer Funktion punktsymmetrisch zu einem gegebenen Punkt P(a|b) ist. Die Anwendung wird an einem Beispiel vorgemacht. | auf teilen
m13v0544 In diesem Video wird die Gleichung hergeleitet, mit der man rechnerisch prüfen kann, ob der Graph einer Funktion punktsymmetrisch zu einem gegebenen Punkt P(a|b) ist. Die Anwendung wird an einem Beispiel vorgemacht. | auf teilen

Gerade und ungerade Funktionen: Symmetrieverhaltung untersuchen von zusammengesetzten Funktionen
m13v0649 Bei dieser Aufgabe geht es um die Symmetrieuntersuchung einer zusammengesetzten Funktion. Man kennt das Symmetrieverhalten der Funktionen f und g, und man soll jetzt das Symmetrieverhalten der aus f und g zusammengesetzten Funktion h ergründen. Dies ist ein Video aus der Serie "So ähnlich im Abi gesehen". | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon
m13v0649 Bei dieser Aufgabe geht es um die Symmetrieuntersuchung einer zusammengesetzten Funktion. Man kennt das Symmetrieverhalten der Funktionen f und g, und man soll jetzt das Symmetrieverhalten der aus f und g zusammengesetzten Funktion h ergründen. Dies ist ein Video aus der Serie "So ähnlich im Abi gesehen". | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon
Das Kapitel „Einführung in den Funktionsbegriff“ ist im Moment noch recht kurz und wird in Zukunft Schritt für Schritt weiter ausgebaut. Viele grundlegende Aspekte zum Thema Funktionen findest du bereits in den Kapiteln zu den einzelnen Funktionstypen (lineare Funktionen, quadratische Funktionen, Exponentialfunktionen usw.).
In den nächsten Erweiterungen dieses Kapitels werden u. a. folgende Themen ergänzt:
- Definition einer Funktion (Zuordnungsvorschrift, Definitions- und Wertebereich)
- Darstellungsformen von Funktionen: Term, Tabelle, Graph, Sachkontext
- Typische Eigenschaften von Funktionen (Monotonie, Beschränktheit, Stetigkeit, Umkehrbarkeit)
- Transformationen von Funktionen (Verschiebungen, Streckungen, Spiegelungen)
- Verknüpfung von Funktionen (Addition, Multiplikation, Verkettung)
- Überblick über verschiedene Funktionsarten, inkl. Spezialfälle (z. B. konstante und abschnittsweise definierte Funktionen)
So entsteht nach und nach ein umfassender Überblick, der dir die Grundlagen des Funktionsbegriffs systematisch vermittelt.