Vektorielle Darstellung von Geraden
Die Parametergleichung einer Geraden: Aufstellen und Verstehen
Die Parametergleichung ist die Standardform, um eine Gerade im dreidimensionalen Raum darzustellen. Sie besteht aus einem Stützvektor, der einen Punkt auf der Geraden fixiert, und einem Richtungsvektor, der die Richtung der Geraden angibt, multipliziert mit einem Parameter. In diesem Abschnitt lernst du, wie du so eine Geradengleichung aufstellst, auch wenn dir nur zwei Punkte gegeben sind, und wie du verschiedene Darstellungsformen von Geraden umwandeln kannst.

m13v0046 In diesem Video wird ein ganz wichtiger Grundaufgabentyp der Vektorrechnung erklärt: das Aufstellen einer Geradengleichung, wenn zwei Punkte gegeben sind.
| auf teilen

m13v0056 In dieser zweiteiligen Videoserie kannst du dein Wissen über die vektorielle Darstellung von Geraden im Raum testen. Hier geht es (1.) um das Aufstellen einer Gleichung, wenn Punkt und Richtung gegeben sind; (2.) der Bestimmung von Punkten, die auf einer Geraden liegen, und (3.) um alternative Darstellungen ein und derselben Geraden. | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon

m13v0376 Bei diesem Übungsvideo geht es um das Aufstellen einer Geradengleichung, das Durchführen einer Punktprobe und die Zerlegung einer Strecke entsprechend eines bestimmten Teilungsverhältnisses. Dieses Video ist aus der Reihe "So ähnlich im Abi gesehen". Eine ähnliche Aufgabe kam im Abitur in Bayern im Jahr 2017 im hilfsmittelfreien Teil dran. | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon
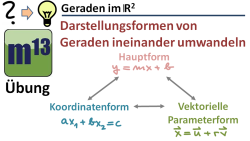
m13v0387 Aus der Mittelstufe kennst du die klassische Hauptform der Geradengleichung y=mx+b. Doch mittlerweile kennst du neben der Koordinatenform auch die vektorielle Parameterdarstellung. In diesem Video soll die Umwandlung zwischen "klassischer" Hauptform, Koordinatenform und Parameterform geübt werden. | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon
Die Punktprobe: Liegt ein Punkt auf der Geraden?
Eine zentrale Aufgabe in der Vektorrechnung ist die Punktprobe, bei der du überprüfst, ob ein gegebener Punkt auf einer bestimmten Geraden liegt. Du lernst hier verschiedene Methoden kennen, darunter den klassischen Ansatz über eine Vektorgleichung und die Vektorvergleichsmethode, die auf Kollinearität basiert.

m13v0047 Die Punktprobe gehört zu den typischen Aufgaben: hierbei wir untersucht, ob ein gegebener Punkt auf der Geraden liegt. | auf teilen
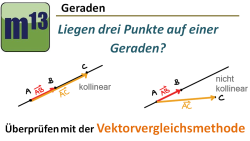
m13v0539 In diesem Video wird eine andere Methode gezeigt, wie man an die Aufgabenstellungen "Liegt ein Punkt auf einer gegebenen Geraden?" oder "Liegen drei Punkte auf einer Geraden?" herangehen kann - die Vektorvergleichsmethode. Beim klassischen Lösungsansatz führte man ja eine Punktprobe über eine Vektorgleichung durch. Bei der Vektorvergleichsmethode vergleicht man zwei ausgewählte Vektoren, ob sie kollinear sind. Wie das geht, wird im Video gezeigt. | auf teilen
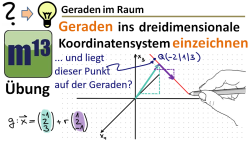
m13v0388 Bei dieser Aufgabe soll eine Gerade und Geradenpunkte ins dreidimensionale Koordinatensystem eingezeichnet werden. Interessant wird es, wenn ein weiterer Punkt ins Koordinatensystem eingezeichnet wird, der aber nur scheinbar auch auf der Geraden liegt. Kannst du erklären was hier los ist? | auf teilen
Arbeitsblatt zum Download
Besondere Lagen von Geraden im Raum
Geraden können im dreidimensionalen Raum spezielle Orientierungen zu den Koordinatenachsen und -ebenen haben. Das Erkennen und Formulieren dieser besonderen Lagen ist super wichtig, damit du die Raumgeometrie tiefer verstehst und es dir leichter fällt, weitere Aufgaben zu lösen.

m13v0644 Eine Gerade mit besonderer Lage im Raum lässt sich am Stütz- und Richtungsvektor auch ohne Rechnung, nur durch "einfaches Hingucken" erkennen. In diesem Video gibt es fünf Beispiele solcher Geraden - erkennst du die besondere Lage im Koordinatensystem? | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon
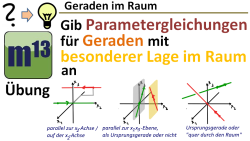
m13v0515 Mit dieser Übung kannst du überprüfen, ob du verstanden hast, welche besonderen Features Geraden mit besonderer Lage im Koordinatensystem haben. Besondere Lagen sind hier Parallelität zu Koordinatenachsen und Koordinatenebenen oder ob sie Ursprungsgeraden sind. Du sollst jeweils zwei verschiedene Gleichungen für Geraden aufstellen, die eine vorgegebene besondere Lage haben. | auf teilen
Arbeitsblatt zum Download

m13v0684 Dies ist eine Aufgabe aus der Reihe "Mathematisches Schnellkrafttraining": Bei dieser Aufgabe geht es darum, durch einen geeigneten Richtungsvektor eine besondere Lage einer Geraden im Koordinatensystem zu erzeugen. | auf teilen
Arbeitsblatt zum Download

m13v0696 Ein weiteres Video aus der Serie "So ähnlich im Abi gesehen". Hier soll die Gleichung einer Geraden mit besonderer Lage im Koordinatensystem aufgestellt werden. | auf teilen
Arbeitsblatt zum Download

m13v0057 In diesem zweiten Wissens-Check-Video zum Thema Geraden geht es um Geraden mit besonderer Lage und Konstruktionsaufgaben. | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon
Spurpunkte und Projektionen von Geraden
Damit du den Verlauf einer Geraden im dreidimensionalen Raum visuell besser verstehen kannst, sind Spurpunkte und Projektionen wichtige Konzepte. Spurpunkte sind die Schnittpunkte einer Geraden mit den Koordinatenebenen und helfen, die Lage der Geraden im Raum zu veranschaulichen.
Dieser Abschnitt zeigt dir, wie du die Spurpunkte einer Geraden berechnest und wie die Anzahl der Spurpunkte von der besonderen Lage der Geraden abhängt. Außerdem lernst du, Geraden auf Koordinatenebenen zu projizieren.

m13v0048 In diesem Video erfährst du, wie man die Spurpunkte einer Geraden (das sind die Schnittpunkte der Geraden mit den drei Koordinatenebenen) berechnet. | auf teilen

m13v0639 Den Verlauf einer Geraden im Raum kann man sehr gut anhand der Spurpunkte darstellen. Bei dieser Aufgabe sollst du genau dies machen - aber Achtung, es werden interessante Fälle behandelt und bei einer Geraden kann man keine Spurpunkte einzeichnen. Es lohnt sich auf jeden Fall, alle vier Aufgaben zu bearbeiten... | auf teilen
Arbeitsblatt zum Download

m13v0624 Eine Gerade im Raum kann 1 bis 3 Spurpunkte haben - wie viele Spurpunkte es gibt, hängt von der (besonderen) Lage der Gerade ab. Bei dieser Aufgabe hast du jetzt zwei Spurpunkte gegeben, und du sollst zunächst begründet und ohne Rechnung entscheiden, ob es einen dritten Spurpunkt gibt. Hier musst du also wissen, wie man anhand zweier Geradenpunkte erkennt, ob die Gerade eine besondere Lage hat... | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon
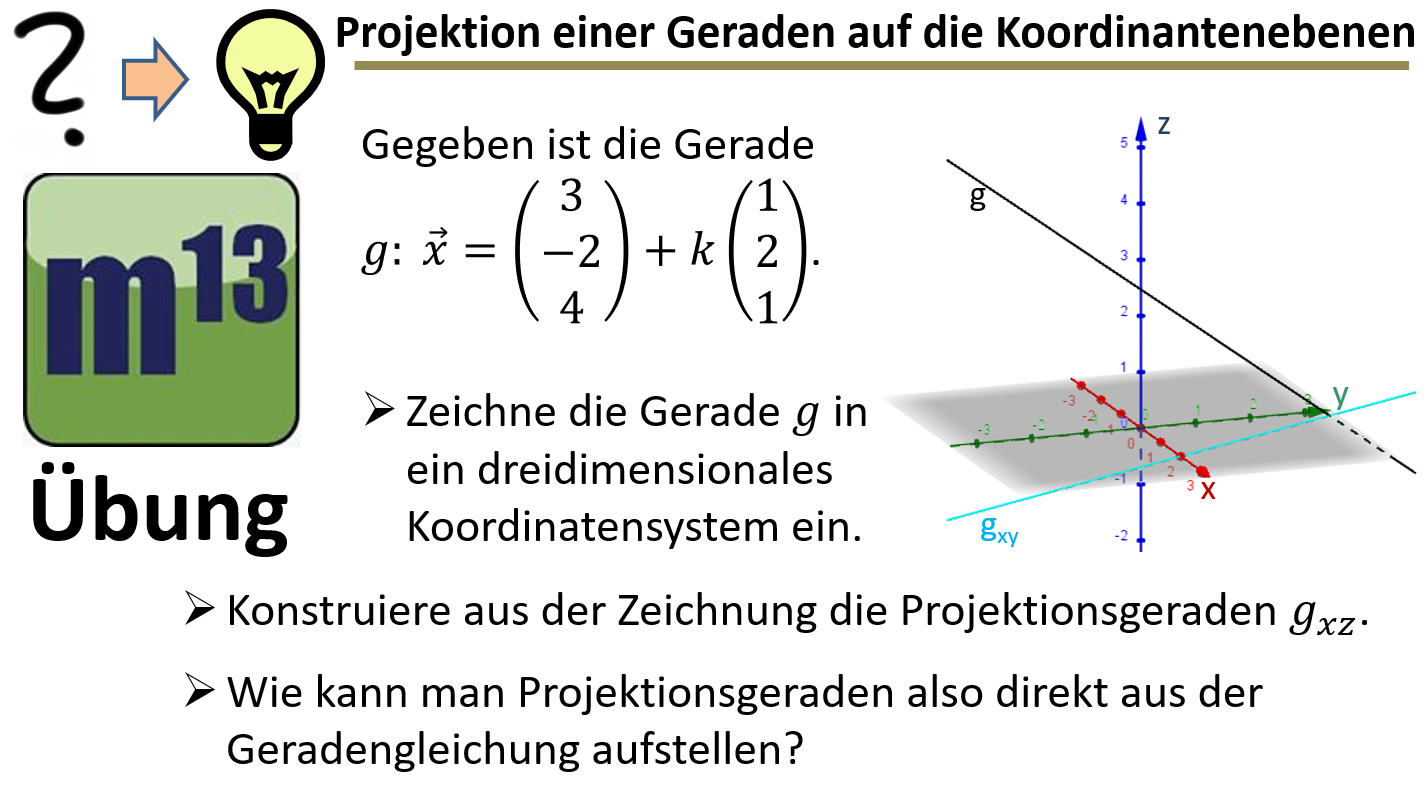
m13v0835 In diesem Video erarbeitest du, wie man eine Gerade im dreidimensionalen Koordinatensystem auf die Koordinatenebenen projiziert. Dabei bestimmst du zunächst eine Projektionsgerade graphisch und leitest anschließend eine allgemeine Methode ab, um Projektionsgleichungen direkt aus der Parameterdarstellung einer Geraden anzugeben. | auf teilen
Arbeitsblatt zum Download
Gegenseitige Lage von Geraden im Raum
Die Untersuchung der gegenseitigen Lage von zwei Geraden im Raum ist ein immer wieder prüfungsrelevanter Grundaufgabentyp. Zwei Geraden im Raum können vier Arten von Beziehungen zueinander haben: Sie können identisch, parallel, windschief zueinander sein, oder sie können sich in einem Schnittpunkt schneiden. Da ein und dieselbe Gerade durch unendlich viele Gleichungen beschrieben werden kann, ist es wichtig, ein systematisches Vorgehen zu kennen, um ihre Lage zueinander zu bestimmen.
In diesem umfassenden Abschnitt lernst du zwei Hauptmethoden kennen, um die gegenseitige Lage von zwei Geraden zu untersuchen: ein systematisches zweistufiges Verfahren und die Methode über das Lösen eines Linearen Gleichungssystems. Du wirst lernen, wie du für jeden der vier Fälle den Nachweis führst und gegebenenfalls den Schnittpunkt bestimmst.

m13v0049 Einführungsvideo zur Untersuchung der gegenseitigen Lage zweier Geraden im Raum. | auf teilen

m13v0051 In diesem Video wird gezeigt, wie man nachweist, dass zwei Geraden identisch sind. | auf teilen

m13v0052 In diesem Video wird gezeigt, wie man nachweist, dass zwei Gereaden (echt) parallel sind. | auf teilen

m13v0053 In diesem Video wird gezeigt, wie man nachweist, dass sich zwei Geraden schneiden und wie man den Schnittpunkt bestimmt. | auf teilen

m13v0054 In diesem Video wird gezeigt, wie man nachweist, dass zwei Geraden windschief zueinander verlaufen. | auf teilen
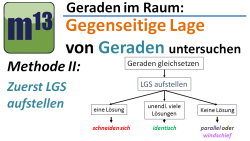
m13v0140 In dem ersten Video und den 4 Beispielvideos wurde ein systematisches, zweistufiges Verfahren zur Untersuchung der gegenseitigen Lage zweier Geraden ausführlich vorgemacht. Dabei wurde im ersten Schritt durch Betrachtung der Richtungsvektoren eine Vorauswahl in zwei Gruppen (identisch, parallel) oder (schneidend, windschief) durchgeführt und im nächsten Schritt zwischen den beiden verbleibenden Möglichkeiten unterschieden.
Man kann jedoch auch einen anderen Weg einschlagen. Hierzu werden die beiden Geradengleichungen im ersten Schritt gleichgesetzt und das zugehörige Lineare Gleichungssystem gelöst. Dann gibt es drei Möglichkeiten:
1. das LGS hat genau eine Lösung. Dann schneiden sich die Geraden in einem Punkt
2. das LGS hat unendlich viele Lösungen. Dann sich die beiden Geraden identisch
3. das LGS hat keine Lösung. In diesem Fall verlaufen die Geraden parallel oder windschief zueinander (und haben so keinen gemeinsamen Punkt).
| auf teilen

m13v0461 Bei dieser Aufgabe hast du zwei Geradengleichungen in Parameterform gegeben und du sollst ohne Rechnung erkennen, ob die Geraden einen Schnittpunkt haben, und wenn ja, welchen. Dabei sollst du dein Wissen anwenden, mit dem du die gegenseitige Lage von Geraden untersuchst. | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon

m13v0676 Hier sollst du nachweisen, dass sich zwei Geraden schneiden, und der Schnittpunkt soll bestimmt werden. Das Besondere bei dieser Aufgabe ist, dass in den Geradengleichungen keine konkreten Vektoren vorkommen, sondern dass du mit "allgemeinen Vektoren" rechnen musst... | auf teilen
Arbeitsblatt zum Download

m13v0833 Bei dieser Aufgabe sollst du zwei Geraden in Parameterform hinsichtlich ihrer Lage untersuchen. Dabei sind in beiden Geradengleichungen dieselben zwei Vektoren enthalten ? jedoch einmal als Stütz- und einmal als Richtungsvektor vertauscht. Mithilfe einer Skizze sollst du geometrisch begründen, dass sich die Geraden in einem Punkt schneiden, und einen Berechnungsterm für den Schnittpunkt angeben. | auf teilen
Arbeitsblatt zum Download
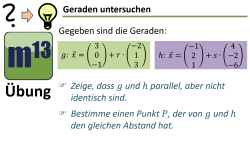
m13v0728 Dies ist eine Aufgabe zum Nachweis, dass zwei Geraden im Raum parallel zueinander sind. Außerdem soll ein Punkt bestimmt werden, der von beiden Geraden den gleichen Abstand hat. | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon

m13v0801 Bei dieser Aufgabe sollst du die gegenseitige Lage zweier Geraden im Raum analysieren. Es geht darum, verschiedene Aussagen zur Beziehung zwischen den Richtungs- und Stützvektoren der Geraden zu bewerten und zu begründen, ob diese wahr oder falsch sind. Dabei musst du dein Wissen über die Eigenschaften von Geraden, insbesondere zu Kollinearität, Schnittpunkten und windschiefen Lagen, anwenden. | auf teilen
Arbeitsblatt zum Download
Geradenscharen
Wenn innerhalb des Stütz- und/oder Richtungsvektors einer Geradengleichung ein weiterer Parameter auftaucht, spricht man von einer Geradenschar. Diese Scharen repräsentieren eine Familie von Geraden, die bestimmte gemeinsame Eigenschaften haben. In diesem Abschnitt würden typische Aufgaben zu Geradenscharen behandelt.
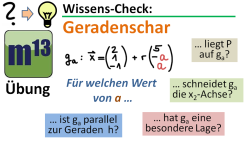
m13v0269 In dieser Übungsaufgabe wird eine Geradenschar bezüglich mehrerer ihrer Eigenschaften in Abhängigkeit des Scharparameters untersucht.
| auf teilen
Arbeitsblatt zum Download
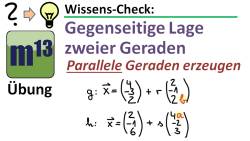
m13v0264 In dieser Übungsaufgabe sollen Geradengleichungen so verändert werden, dass die Geraden parallel zueinander liegen. Hierbei kannst du deine Kenntnisse zur gegenseitigen Lage von Geraden prüfen. | auf teilen
Arbeitsblatt zum Download
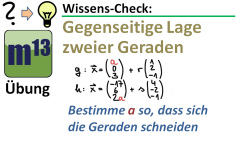
m13v0268 In dieser Aufgaben hat man zwei Geradenscharen gegeben, und man soll den Scharparameter so bestimmen, dass die Geraden sich schneiden. | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon
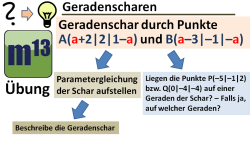
m13v0426 Ein weiteres Übungsvideo zu Geradenscharen. Hier geht es darum, die Gleichung einer Geradenschar aufzustellen und zu prüfen, ob ein gegebener Punkt auf einer der Geraden der Schar liegt, und falls ja, diese Gerade zu identifizieren. | auf teilen
Arbeitsblatt zum Download
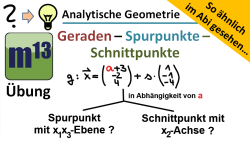
m13v0373 In diesem Übungsvideo geht es um die Bestimmung der Schnittpunkte einer Gerade mit einer Koordinatenebene (Spurpunkt) bzw. einer Koordinatenachse. Da die vektorielle Gleichung der Geraden in diesem Fall einen zusätzlichen Parameter im Stützvektor enthält, hängt die Ermittlung der gesuchten Schnittpunkte von diesem Parameter ab. Dies macht das Problem natürlich ein bisschen anspruchsvoller...
Dies ist ein Video aus der Serie "So ähnlich im Abi gesehen"; eine ähnliche Aufgabe wurde im Abi des Landes Bayern im Jahr 2018 gestellt. | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon
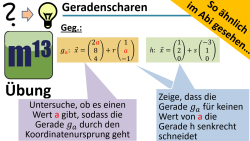
m13v0726 Zwei Aufgaben zur Untersuchung einer Geradenschar. Dies ist ein Video aus der Reihe "So ähnlich im Abi gesehen". | auf teilen
Arbeitsblatt zum Download
Nachdem du die Vektoraddition, die S-Multiplikation und die Linearkombination von Vektoren kennengelernt hast, tauchst du jetzt in die erste wichtige Anwendung der Vektorrechnung ein: die Beschreibung von Geraden im Raum mittels Parametergleichungen. Geraden sind ein fundamentaler Bestandteil der analytischen Geometrie und werden in vielen Klausuren abgefragt.