Das Vektorprodukt (auch Kreuzprodukt genannt)
Einführung und Berechnungsmethoden
Bevor es an die Anwendungen geht, lernst du, wie man das Vektorprodukt überhaupt berechnet und welche Grundidee dahinter steckt.

m13v0042 In Lehrbüchern und Formelsammlungen findet man eine komplizierte Formel zur Berechnung des Vektorprodukts. In diesem Video wird eine pfiffige Methode vorgestellt, mit der man schnell und übersichtlich das Vektorprodukt zweier Vektoren bestimmen kann, ohne diese Formel auswendig lernen zu müssen. | auf teilen
Eigenschaften des Vektorprodukts
Damit du das Vektorprodukt sicher anwenden kannst, ist es wichtig, seine Eigenschaften zu kennen. Dazu gehören Orthogonalität, Vorzeichenverhalten und die Frage nach Gesetzen wie dem Assoziativgesetz.

m13v0632 Bei dieser Aufgabe sollst du rechnerisch (und allgemein) nachweisen, dass der durch die Berechnungsformel Vektor(a)×Vektor(b) gegebene Vektor gleichzeitig senkrecht zu den Vektoren a und b ist. | auf teilen
Arbeitsblatt zum Download

m13v0637 In dieser Übungsaufgabe geht es darum, die Eigenschaft der Antikommutativität des Vektorprodukts (Kreuzprodukts) zu beweisen. Dazu sollen zwei beliebige Vektoren ausgewählt werden, und das Vektorprodukt beider Vektoren in beiden Reihenfolgen berechnet werden. Anschließend sollen die beiden Ergebnisse verglichen werden, um zu zeigen, dass sie zwar unterschiedlich sind, jedoch das negative Vorzeichen voneinander haben. | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon

m13v0773 In dieser Aufgabe geht es darum, anhand eines konkreten Beispiels zu überprüfen, ob für das Vektorprodukt das Assoziativgesetz gilt. | auf teilen
Arbeitsblatt zum Download
Anwendungen in der Geometrie
Das Vektorprodukt ist ein mächtiges Werkzeug zur Lösung geometrischer Probleme.
Normalenvektoren
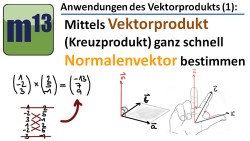
m13v0260 Manchmal sucht man einen Vektor, der gleichzeitig senkrecht zu zwei gegebenen Vektoren steht. Dies ist ein sogenannter Normalenvektor. Mit Hilfe des Vektorproduktes kann man einen solchen Normalenvektor bestimmen. Die Bestimmung eines Normalenvektors ist zum Beispiel wichtig, wenn kann die Parametergleichung einer Ebene in die Normalenform (oder Koordinatenform) umwandeln möchte. | auf teilen
Flächen und Höhen
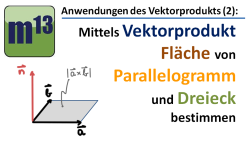
m13v0261 In diesem Video wird gezeigt, wie man mit Hilfe des Vektorprodukts (auch Kreuzprodukt genannt) sehr einfach den Flächeninhalt von Parallelogramm und Dreieck bestimmen kann. Ein Parallelogramm werden durch zwei Vektoren aufgespannt. Das Vektorprodukt dieser Aufspannvektoren ergibt einen Vektor, dessen Betrag (also Länge) dem Flächeninhaltswert des aufgespannten Parallelogramms entspricht. Wenn man berücksichtigt, dass ein Dreieck ebenfalls durch zwei Vektoren aufgespannt wird, welches die halbe Fläche des entsprechenden Parallelogramms hat, kann man über das Vektorprodukt der Aufspannvektoren auch die Fläche des Dreiecks bestimmen. Im Video wird es genau erklärt - auch mit Beispielen. | auf teilen
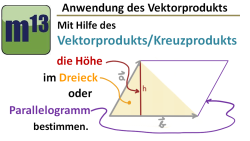
m13v0391 In diesem Video wird eine weitere Anwendung des Vektorprodukts (Kreuzprodukts) gezeigt: Die Bestimmung der Höhe in einem Dreieck bzw. Parallelogramm.
Wir hatten ja schon in einem früheren Video gesehen, dass sich mit Hilfe des Vektorprodukts sehr einfach die Fläche eines Parallelogramms bzw. Dreiecks ermitteln lässt. Die elementargeometrischen Formeln zur Berechnung der Fläche von Dreieck (bzw. Parallelogramm) lässt sich nach der Höhe auflösen. Drückt man dann die Grundseite als Vektor aus und nimmt dessen Betrag, so gelangt man zu einer Formel für die Höhe. Das Video zeigt, wie das geht. | auf teilen
Volumen

m13v0529 Ein Spat ist ein Körper, der durch drei Vektoren (die nicht in einer Ebene liegen) aufgespannt wird. In diesem Video wird das sogenannte Spatprodukt hergeleitet - dies ist eine Kombination von Vektorprodukt und Skalarprodukt. Über das Spatprodukt lässt sich sehr einfach das Volumen eines Spats bestimmen. Im Video wird die Spatprodukt-Formel hergeleitet, und es wird ein Anwendungsbeispiel gezeigt. | auf teilen
Übungsaufgaben zum Rechnen mit dem Vektorprodukt
Hier kannst du überprüfen, ob du das Vektorprodukt verstanden hast und es in Gleichungen einsetzen kannst.

m13v0658 Eine Aufgabe, mit der du überprüfen kannst, ob du das Rechnen mit dem Vektorprodukt verstanden hast. In der Vektorproduktgleichung kommen die Parameter a, b und c vor, deren Werte du bestimmen sollst, so dass die Gleichung erfüllt ist. | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon
Vertiefung: Verbindungen zu anderen Rechenoperationen
Das Vektorprodukt steht in engem Zusammenhang mit dem Skalarprodukt und allgemeinen Vektorgleichungen. Diese Videos vertiefen dein Verständnis.

m13v0634 In der Vektorrechnung gibt es die Multiplikation in mehrfacher Form: als (1) Multiplikation zwischen Skalar und Vektor, (2) als Skalarprodukt zweier Vektoren und (3) als Vektorprodukt. Für die Fälle (1) und (2) wird oft der "normale" Malpunkt "∙" verwendet. Bei dieser Aufgabe sollst du Rechenausdrücke dahingehend überprüfen, ob das Ergebnis ein Skalar ist oder ein Vektor, oder ob der Ausdruck gar sinnvoll ist. | auf teilen
Arbeitsblatt zum Download

m13v0687 Bei diesem Video aus der Serie "Mathematisches Schnellkrafttraining" geht es um die geometrische Interpretation von Gleichungen, die das Vektor und Skalarprodukt enthalten. | auf teilen
Arbeitsblatt zum Download
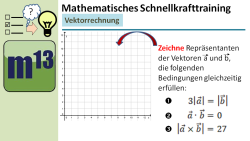
m13v0625 Es sind drei Vektorgleichungen gegeben, die für zwei Vektoren gleichzeitig erfüllt sein sollen. Interpretiere die geometrische Bedeutung dieser Gleichungen und zeichne Repräsentanten der Vektoren, die diese Bedingungen alle erfüllen, ins Koordinatensystem. Ein Video aus der neuen "MST-Reihe" - momentan noch ein Extra für Level 2-Kanalmitglieder... | auf teilen
Arbeitsblatt zum Download
Anwendungen auf Geraden und Lagenbeziehungen
Mit Hilfe des Vektor- und Spatprodukts kann man auch die gegenseitige Lage von Geraden untersuchen.

m13v0677 Mit dieser Aufgabe kannst du prüfen, ob du die Zusammenhänge zwischen gegenseitiger Lage von Geraden, lineare Abhängigkeit und Vektorprodukt der in den Geradengleichungen vorkommenden Vektoren verstanden hast. | auf teilen
Arbeitsblatt zum Download
Das Vektorprodukt (oder auch Kreuzprodukt) ist eine Verrechnungsart von Vektoren, die als Ergebnis einen Vektor liefert (im Gegensatz zum Skalarprodukt, bei dem aus der Verrechnung zweier Vektoren eine Zahl entsteht).
Das Vektorprodukt ist wichtig für viele Anwendungen, z.B. die schnelle Ermittlung von Normalenvektoren (wichtig bei der Aufstellung von Ebenengleichungen) oder für Flächen- und Volumenberechnungen. Sogar für verschiedene Arten der Abstandsberechnung zwischen Punkt, Gerade und Ebene lässt sich das Vektorprodukt verwenden.
In der Schule wird das Vektorprodukt manchmal im Grundkurs nicht behandelt - schade eigentlich, denn es macht viele ansonsten umständlicher Berechnungsmethoden einfacher.