Lineare Funktionen
Die Grundlagen Linearer Funktionen verstehen
Geraden grafisch darstellen und ihre Eigenschaften analysieren
Geradengleichung gegeben → Gerade zeichnen
m13v0421 Eine Aufgabe, wie sie in jeder Einstiegsklausur zum Thema Lineare Funktionen drankommt: Es ist die Funktionsgleichung gegeben und man soll die Funktion ins Koordinatensystem einzeichnen. | auf teilen
m13v0421 Eine Aufgabe, wie sie in jeder Einstiegsklausur zum Thema Lineare Funktionen drankommt: Es ist die Funktionsgleichung gegeben und man soll die Funktion ins Koordinatensystem einzeichnen. | auf teilen

Nullstellen und y-Achsenabschnitt von Geraden bestimmen
m13v0020 Eine Gerade (die nicht waagerecht verläuft) schneidet die Koordinatenachsen in zwei Punkten. Der y-Wert, wo die Gerade die y-Achse schneidet, wird y-Achsenabschnitt genannt; der x-Wert, wo die x-Achse geschnitten wird, bezeichnet man geläufig als Nullstelle. Hier wird gezeigt, wie man die Schnittpunkte mit den Koordinatenachsen rechnerisch bestimmt. | auf teilen
m13v0020 Eine Gerade (die nicht waagerecht verläuft) schneidet die Koordinatenachsen in zwei Punkten. Der y-Wert, wo die Gerade die y-Achse schneidet, wird y-Achsenabschnitt genannt; der x-Wert, wo die x-Achse geschnitten wird, bezeichnet man geläufig als Nullstelle. Hier wird gezeigt, wie man die Schnittpunkte mit den Koordinatenachsen rechnerisch bestimmt. | auf teilen

Steigungswinkel einer Geraden bestimmen
m13v0121 Man bezeichnet den Winkel zwischen einer Gerade und der x-Achse als den Steigungswinkel der Geraden. Dabei wird der Winkel im mathematisch positiven Sinn gemessen: dies ist der Winkel der überstrichen wird, wenn man von der x-Achse im entgegengesetzten Uhrzeigesinn dreht, bis man zur Geraden gelangt. Wie der Steigungswinkel mit der Steigung zusammenhängt, erfährst du in diesem Video. | auf teilen
m13v0121 Man bezeichnet den Winkel zwischen einer Gerade und der x-Achse als den Steigungswinkel der Geraden. Dabei wird der Winkel im mathematisch positiven Sinn gemessen: dies ist der Winkel der überstrichen wird, wenn man von der x-Achse im entgegengesetzten Uhrzeigesinn dreht, bis man zur Geraden gelangt. Wie der Steigungswinkel mit der Steigung zusammenhängt, erfährst du in diesem Video. | auf teilen
Geradengleichungen aus gegebenen Informationen aufstellen

Geradengleichung aufstellen: Punkt und Steigung gegeben
m13v0120 Wie man eine Geradengleichung (y=mx+b) bestimmt, wenn Punkt und Steigung gegeben sind, wird in diesem Video vorgemacht.
| auf teilen
m13v0120 Wie man eine Geradengleichung (y=mx+b) bestimmt, wenn Punkt und Steigung gegeben sind, wird in diesem Video vorgemacht.
| auf teilen

Geradengleichung aufstellen: Gerade durch 2 Punkte
m13v0021 Eine Gerade ist eindeutig durch zwei Punkte festgelegt. Also muss es eine Möglichkeit geben, aus zwei gegebenen Punkten die zugehörige Geradengleichung aufzustellen. Hier wird eine Methode gezeigt, wie man es machen kann. | auf teilen
m13v0021 Eine Gerade ist eindeutig durch zwei Punkte festgelegt. Also muss es eine Möglichkeit geben, aus zwei gegebenen Punkten die zugehörige Geradengleichung aufzustellen. Hier wird eine Methode gezeigt, wie man es machen kann. | auf teilen
Spezielle Formen der Geradengleichung kennenlernen
Neben der Hauptform y=mx+b gibt es weitere Darstellungsformen für Geradengleichungen, die je nach Aufgabenstellung praktisch sein können. Du lernst, wie du diese Formen anwendest und in die Hauptform umwandelst.

Die Punkt-Steigungsform der Geradengleichung
m13v0517 Die Punkt-Steigungsform der Geradengleichung ist eine praktische Darstellungweise einer Linearen Funktion, in der man direkt die Steigung und die Punkt-Koordinaten einsetzen kann. In wenigen Schritten gelangt man von der Punkt-Steigungsform zur geläufigen Hauptform der Geradengleichung. | auf teilen
m13v0517 Die Punkt-Steigungsform der Geradengleichung ist eine praktische Darstellungweise einer Linearen Funktion, in der man direkt die Steigung und die Punkt-Koordinaten einsetzen kann. In wenigen Schritten gelangt man von der Punkt-Steigungsform zur geläufigen Hauptform der Geradengleichung. | auf teilen
Zwei-Punkte-Form der Geradengleichung
m13v0524 Eine Gerade ist durch zwei Punkte eindeutig bestimmt. Die Zwei-Punkte-Form ist eine spezielle Form der Geradengleichung, in die man die Koordinaten der beiden Punkte einsetzen kann und nach etwas Umformen die Geradengleichung in der Standardform erhält. Im Video wird an zwei Beispielen die Anwendung gezeigt, und außerdem wird die Herleitung der Zwei-Punkte-Form besprochen. | auf teilen
m13v0524 Eine Gerade ist durch zwei Punkte eindeutig bestimmt. Die Zwei-Punkte-Form ist eine spezielle Form der Geradengleichung, in die man die Koordinaten der beiden Punkte einsetzen kann und nach etwas Umformen die Geradengleichung in der Standardform erhält. Im Video wird an zwei Beispielen die Anwendung gezeigt, und außerdem wird die Herleitung der Zwei-Punkte-Form besprochen. | auf teilen
Die Achsenabschnittsform der Geradengleichung
m13v0526 Eine Gerade, welche die x- und die y-Achse schneidet, ist durch die beiden Schnittpunkte mit den Achsen eindeutig bestimmt. Bei der sogenannten Achsenabschnittsform der Geradengleichung wird die Gerade durch die Achsenabschnitte beschrieben. Ausgehend von der Achsenabschnittsform kann man in wenigen Umformungsschritten zur Hauptform gelangen. | auf teilen
m13v0526 Eine Gerade, welche die x- und die y-Achse schneidet, ist durch die beiden Schnittpunkte mit den Achsen eindeutig bestimmt. Bei der sogenannten Achsenabschnittsform der Geradengleichung wird die Gerade durch die Achsenabschnitte beschrieben. Ausgehend von der Achsenabschnittsform kann man in wenigen Umformungsschritten zur Hauptform gelangen. | auf teilen

Die Koordinatenform der Geradengleichung
m13v0532 Die Koordinatenform ist eine spezielle Form der Geradengleichung, bei der die Terme mit den Variablen x und y auf der einen Seite der Gleichung stehen und ein Zahlenterm auf der anderen Seite. Die Gleichung ist für alle Geradenpunkte erfüllt, d.h. wenn man die x- und y-Koordinate eines beliebigen Geradenpunktes in die Gleichung einsetzt, erhält man eine wahre Aussage. Die Koordinatenformen von Geraden spielen eine wichtige Rolle beim Lösen von Linearen Gleichungssystemen, so wie man es in der Mittelstufe lernt. | auf teilen
m13v0532 Die Koordinatenform ist eine spezielle Form der Geradengleichung, bei der die Terme mit den Variablen x und y auf der einen Seite der Gleichung stehen und ein Zahlenterm auf der anderen Seite. Die Gleichung ist für alle Geradenpunkte erfüllt, d.h. wenn man die x- und y-Koordinate eines beliebigen Geradenpunktes in die Gleichung einsetzt, erhält man eine wahre Aussage. Die Koordinatenformen von Geraden spielen eine wichtige Rolle beim Lösen von Linearen Gleichungssystemen, so wie man es in der Mittelstufe lernt. | auf teilen
Beziehungen zwischen Geraden untersuchen
Parallelität und Orthogonalität
Geraden können in speziellen Beziehungen zueinander stehen, wie parallel oder orthogonal. Diese Konzepte sind grundlegend, um geometrische Probleme zu lösen und weitere Geradengleichungen aufzustellen.
Zur gegebener Gerade parallele und orthogonale Geraden so bestimmen, dass diese durch gegebenen Punkt verlaufen
m13v0386 Zu einer gegebenen Gerade gibt es unendlich viele parallele und orthogonale Geraden. In dieser Übungsaufgabe sollst du unter all diesen parallelen bzw. orthogonalen Geraden diejenige bestimmen, die durch einen angegebenen Punkt geht. | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon
m13v0386 Zu einer gegebenen Gerade gibt es unendlich viele parallele und orthogonale Geraden. In dieser Übungsaufgabe sollst du unter all diesen parallelen bzw. orthogonalen Geraden diejenige bestimmen, die durch einen angegebenen Punkt geht. | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon
Schnittpunkte von Geraden bestimmen und das Lösen von linearen Gleichungen
Das Finden des Schnittpunkts von zwei Geraden ist eine zentrale Anwendung linearer Funktionen und führt dich zum Lösen von linearen Gleichungen bzw. Gleichungssystemen. Um Schnittpunkte von Geraden zu bestimmen, musst du lineare Gleichungen sicher lösen können.

Lineare Gleichungen lösen
m13v0789 Diese Aufgabe ermöglicht es dir, deine Kompetenz im Lösen linearer Gleichungen zu überprüfen. Die Aufgaben decken alle möglichen Fälle von Lösungsmengen ab: eine eindeutige Lösung, keine Lösung oder unendlich viele Lösungen. | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon
m13v0789 Diese Aufgabe ermöglicht es dir, deine Kompetenz im Lösen linearer Gleichungen zu überprüfen. Die Aufgaben decken alle möglichen Fälle von Lösungsmengen ab: eine eindeutige Lösung, keine Lösung oder unendlich viele Lösungen. | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon

Wo schneiden sich die beiden Geraden? | Lineare Funktionen (Übung)
m13v0322 In dieser Übungsaufgabe ist nur ein Ausschnitt aus dem Koordinatensystem gezeigt: Dort sind zwei Punkte eingezeichnet, durch die zwei Geraden gehen. Gesucht ist der Schnittpunkt der Geraden, den man nicht direkt aus dem Koordinatensystem ablesen kann. Um die Aufgabe zu lösen, musst du zunächst die Geradengleichungen aufstellen und dann den Schnittpunkt bestimmen. | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon
m13v0322 In dieser Übungsaufgabe ist nur ein Ausschnitt aus dem Koordinatensystem gezeigt: Dort sind zwei Punkte eingezeichnet, durch die zwei Geraden gehen. Gesucht ist der Schnittpunkt der Geraden, den man nicht direkt aus dem Koordinatensystem ablesen kann. Um die Aufgabe zu lösen, musst du zunächst die Geradengleichungen aufstellen und dann den Schnittpunkt bestimmen. | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon
Kompetenzübergreifende und klausurtypische Aufgaben
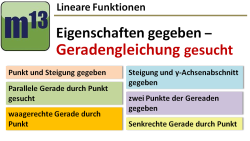
Geradengleichung aufstellen aus gegebenen Eigenschaften der Geraden
m13v0527 Dies ist eine Übungsaufgabe, in der noch einmal alle wichtigen Konstruktionsmöglichkeiten von Geraden behandelt werden. Eine Gerade wird durch durch ihre Eigenschaften beschrieben, und man soll jetzt die Funktionsgleichung der Gerade aufstellen. | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon
m13v0527 Dies ist eine Übungsaufgabe, in der noch einmal alle wichtigen Konstruktionsmöglichkeiten von Geraden behandelt werden. Eine Gerade wird durch durch ihre Eigenschaften beschrieben, und man soll jetzt die Funktionsgleichung der Gerade aufstellen. | auf teilen
Arbeitsblatt zum Download Musterlösung auf Patreon
Linearen Funktionen repräsentieren den einfachsten Typ von Funktionen. Ihre Graphen sind Geraden. In dieser Videoserie lernst du, aus welchen Komponenten eine lineare Funktion aufgebaut ist (Steigung und y-Achsenabschnitt), wie man die entsprechenden Geraden zeichnet bzw. wie man umgekehrt aus dem Graphen die zugehörige Funktionsgleichung ermittelt.
In diesem Kapitel erfährst du alles Wichtige über sie: welche Bausteine sie haben – die Steigung und den y-Achsenabschnitt –, wie du die entsprechenden Geraden zeichnest und wie du umgekehrt aus einem gezeichneten Graphen die zugehörige Funktionsgleichung ermittelst.