Die Normalverteilung

Kurvendiskussion der Gauß'schen Glockenfunktion
m13v0504 In diesem Video wird die Kurvendiskussion der Gaußschen Glockenkurve φ(x) hinsichtlich Definitionsbereich, Nullstellen, Symmetrie, Extrem- und Wendepunkte besprochen. | auf teilen

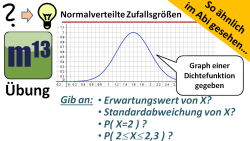
Normalverteilung: Erwartungswert, Standardabweichung, Wahrscheinlichkeiten (So ähnlich im Abi gesehen)
m13v0495 Mit dieser Aufgabe kannst du prüfen, ob du verstanden hast, welche Aussagen die Dichtefunktion einer normalverteilten Zufallsgröße liefert. Aus dem Graphen der Dichtefunktion sollst du Erwartungswert und Standardabweichung sowie Einzel- und Intervallwahrscheinlichkeiten der normalverteilten Zufallsgröße abschätzen. | auf teilen
Arbeitsblatt zum Download

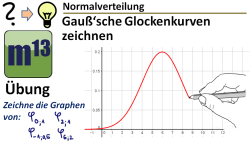
Gauß'sche Glockenkurve zeichnen
m13v0506 Bei dieser Aufgabe sollst du die Graphen von Gaußschen Glockenfunktionen bei vorgegebenem μ und σ zeichnen. Mit dieser Übung kannst du überprüfen, ob du die wesentlichen Eigenschaften der φ_μ;σ-Funktionen verstanden hast. | auf teilen
Arbeitsblatt zum Download

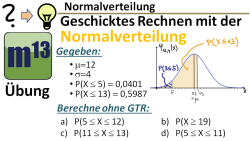
Geschicktes Rechnen mit der Normalverteilung
m13v0513 Bei dieser Übung geht es um das geschickte Rechnen mit der Normalverteilung. Die Werte des Erwartungswertes μ und der Standardabweichung σ sowie zwei Intervallwahrscheinlichkeiten sind gegeben. Jetzt sollst du − und das ist der Clue bei der Aufgabe − unter Ausnutzung von Symmetrieeigenschaften der Normalverteilung weitere Intervallwahrscheinlichkeiten berechnen − ohne Taschenrechner!
Wie das geht, wird im Video vorgemacht. | auf teilen
Arbeitsblatt zum Download

Normalverteilung GTR-Aufgaben (1) - normCdf und invNorm
m13v0508 Zwei typische Aufgaben zur Normalverteilung, die man mit dem GTR lösen kann. Gesucht ist das Intervall der Zufallsgröße X, so dass man einen bestimmten Wahrscheinlichkeitswert erhält. In diesem Video benutze ich als GTR den TI-nspire CX und die Funktionen normCdf und invNorm. | auf teilen
Arbeitsblatt zum Download

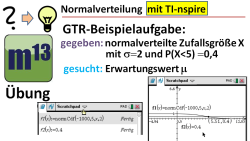
Normalverteilung GTR-Aufgaben (2) - Standardabweichung μ gesucht
m13v0509 Eine weitere Aufgabe zur Normalverteilung, die man mit dem GTR lösen kann: Hier geht es darum, den Erwartungswert μ einer Normalverteilung zu bestimmen, wenn man eine Angabe zur Standardabweichung und eine Intervallwahrscheinlichkeit (σ=2 und P(X | auf teilen
Arbeitsblatt zum Download

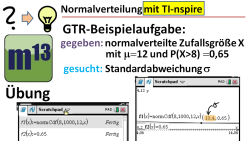
Normalverteilung GTR-Aufgaben (3) - Standardabweichung σ gesucht
m13v0510 Bei dieser Aufgabe soll die Standardabweichung σ einer Normalverteilung bestimmt werden. Dafür stehen folgende Ausgangsinformationen zur Verfügung: Der Erwartungswert μ=12 und die Intervallwahrscheinlichkeit P(X>8)=0,65. Dies ist eine GTR-Aufgabe, die mit dem TI-inspire vorgemacht wird. | auf teilen
Arbeitsblatt zum Download

Wahrscheinlichkeiten mit Sigma-Regeln berechnen
m13v0682 Hier sollen Intervallwahrscheinlichkeiten für eine normalverteilte Zufallsgröße mithilfe der Sigma-Regeln bestimmt werden (dies kann man ohne Taschenrechner machen). | auf teilen
Arbeitsblatt zum Download

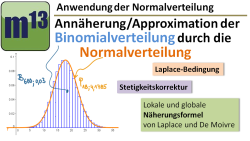
Verwendung der Normalverteilung zur Approximation der Binomialverteilung
m13v0511 Der Graph einer Binomialverteilung wird umso glockenförmiger, je größer n wird. Eine "schöne" Glockenform liegt vor, wenn die Standardabweichung größer 3 ist (Laplace-Bedingung). Jetzt ist die Dichtefunktion einer Normalverteilung ist ja eine glockenförmige Funktion, und so ist es möglich, eine Binomialverteilung durch die Normalverteilung anzunähern. Welche Vorteile dies hat, in wie man damit Einzelwahrscheinlichkeiten und kumulierte Wahrscheinlichkeiten von Binomialverteilungen näherungsweise berechnen kann (lokale bzw. globale Näherungsformel von Laplace und De Moivre), erfährst du in diesem Video. | auf teilen