m13v0369 In diesem Video geht es um die Herleitung des Skalarprodukts. Ausgehend von der Frage, welchen Winkel zwei Vektoren einschließen, macht man sich zunächst klar, dass zwei Vektoren ein Dreieck aufspannen. Mit Hilfe des Kosinussatzes wird dann eine Formel entwickelt, mit der man den Winkel der beiden Vektoren bestimmen kann. In dieser Formel kommt ein besonderer Term vor, den man als sogenanntes Skalarprodukt definiert hat. | auf teilen

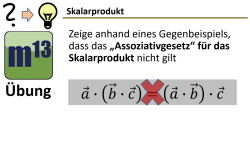
m13v0664 Welche Rechengesetze gelten für das Skalarprodukt? - Zeige durch ein Gegenbeispiel, dass das "Assoziativgesetz" für das Skalarprodukt nicht gilt. Arbeitsblatt zum Download | auf teilen

m13v0220 In diesem Video lernst du, wie man mit Hilfe des Skalarprodukts überprüfen kann, ob zwei Vektoren senkrecht (orthogonal) zueinander stehen. Dies ist eine wichtige Grundanwendung des Skalarprodukts, die in vielfacher Weise angewendet wird. | auf teilen

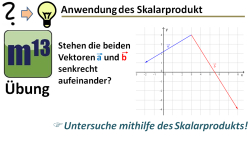
m13v0642 Sind zwei Vektoren, die augenscheinlich senkrecht aufeinander stehen, tatsächlich senkrecht zueinander? - Mit dem Skalarprodukt kann man dies überprüfen... Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen

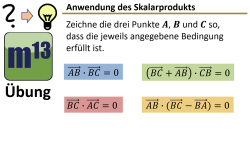
m13v0747 Mit diesen Aufgaben kannst du überprüfen, ob du (1.) das Orthogonalitätskriterium anhand des Skalarproduktes und (2.) die Konstruktion neuer Vektoren durch Vektoraddition bzw. -subtraktion verstanden hast. Arbeitsblatt zum Download | auf teilen

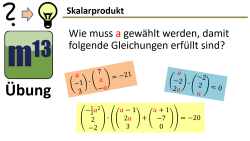
m13v0663 Hier sollst du Vektorgleichungen lösen, in denen das Skalarprodukt vorkommt... Ein häufig vorkommender Aufgabentyp. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen

m13v0221 In diesem Video lernst du, wie man mit Hilfe des Skalarprodukts den Winkel zwischen zwei Vektoren bestimmen kannst. | auf teilen

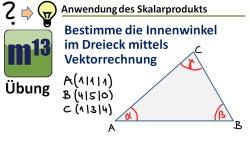
m13v0516 Gegeben sind die Punkte eines Dreiecks und man soll die Innenwinkel bestimmen. Dies ist eine typische Anwendungsaufgabe zur Kosinusformel des Skalarprodukts zur Bestimmung des Winkels zwischen zwei Vektoren. Arbeitsblatt zum Download | auf teilen

m13v0158 Wenn man einen Vektor gegeben hat und ganz schnell irgendeinen Vektor sucht, der zu diesem Vektor senkrecht (orthogonal) steht, so kann man dies ganz ohne Rechnen und ganz schnell machen. Dieses Video zeigt wie das geht. | auf teilen

m13v0432 In diesem Video wird eine interessante Eigenschaft des Skalarproduktes besprochen, nämlich der Zusammenhang zwischen Skalarprodukt und Vektorlänge (Betrag des Vektors). | auf teilen

m13v0782 Rechenregeln, die wir von Zahlen kennen, gelten nicht unbedingt für Vektoren. Hier sollst du zeigen, dass eine Beziehung, die den Potenzgesetzen von Zahlen ähnelt, für das Skalarprodukt zweier Vektoren im Allgemeinen nicht gilt. Unter bestimmten Bedingungen trifft diese Beziehung jedoch zu, und du sollst herausfinden, wann das der Fall ist. Arbeitsblatt zum Download | auf teilen

m13v0643 Mit dieser Aufgabe kannst du prüfen, ob du das Wesen des Skalarproduktes verstanden hast, da hier mehrere Aspekte über das Skalarprodukt zusammengebracht werden müssen, um den Wert eines Vektorterms zu berechnen. Versuche es mal! Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen

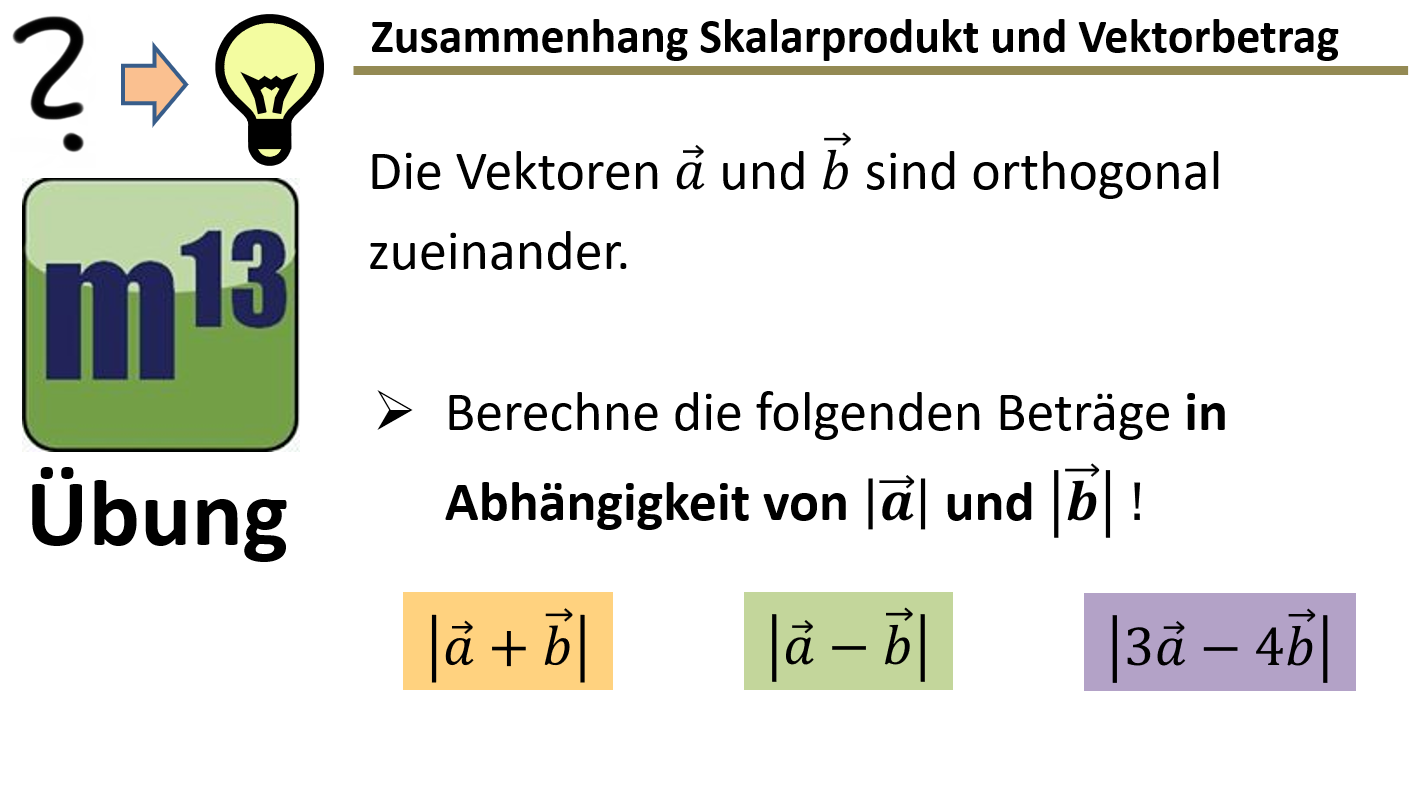
m13v0831 Bei dieser Aufgabe geht es um den Zusammenhang zwischen dem Skalarprodukt und den Längen (Beträgen) von Vektoren. Gegeben ist, dass die beiden vorkommenden Vektoren orthogonal zueinander sind. Nun sollst du die Länge verschiedener Linearkombinationen dieser Vektoren in Abhängigkeit von den Beträgen der Ausgangsvektoren bestimmen. Arbeitsblatt zum Download | auf teilen

m13v0770 In dieser Aufgabe geht es um die Anwendung der Kosinusformel des Skalarprodukts zur Berechnung des Winkels zwischen zwei Vektoren. Auf dem Weg dorthin musst du jedoch an mehreren Stellen dein Wissen über das Skalarprodukt anwenden, insbesondere das Orthogonalitätskriterium und die Rechenregeln, um die erforderlichen Werte zu ermitteln. Arbeitsblatt zum Download | auf teilen

m13v0771 Das Skalarprodukt stellt einen Bezug zwischen den Vektorlängen und dem eingeschlossenen Winkel her und beschreibt somit auch geometrische Eigenschaften der Vektoren. In dieser Aufgabe sind einige Angaben zu zwei Vektoren gegeben. Mit deinem Wissen über die Definition des Skalarprodukts sollst du begründen, warum die Vektoren nicht orthogonal sind, und die Länge eines der Vektoren bestimmen. Arbeitsblatt zum Download | auf teilen

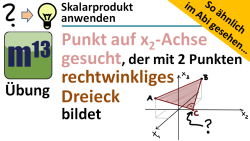
m13v0296 Dieses Übungsvideo behandelt (1.) das Einzeichnen von Punkten ins dreidimensionale Koordinatensystem und (2.) die Anwendung des Skalarproduktes zur Konstruktion eines rechwinkligen Dreiecks. Dies ist ein Video aus der Reihe So ähnlich im Abi gesehen. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen

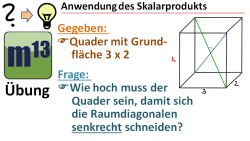
m13v0505 Eine Anwendung des Skalarprodukts: man soll die Höhe eines Quaders bei gegebener Grundfläche so bestimmen, dass sich die Raumdiagonalen senkrecht schneiden. Arbeitsblatt zum Download | auf teilen

m13v0581 Eine Aufgabe aus der Serie "So ähnlich im Abi gesehen", bei der es um die Strategieentwicklung beim Lösungsweg geht. Mehrere Kompetenzen sind hier anzuwenden: Welche Eigenschaften haben parallele Geraden? Wie ist das Orthogonalitätskriterium anzuwenden, um das Lot auf eine Gerade durch einen Punkt zu fällen? Und wie bestimmt man den Abstand paralleler Geraden? Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen

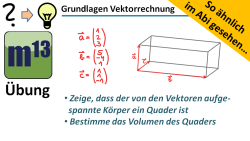
m13v0564 Bei dieser Aufgabe soll ein durch drei Vektoren aufgespannter Körper untersucht werden. Einen Körper, der durch drei Vektoren aufgespannt ist, bezeichnet man als Spat. Hier soll gezeigt werden, dass es sich bei diesem Spat um einen Quader handelt. Außerdem soll das Volumen des Quaders bestimmt werden. Diese Aufgabe soll ohne Hilfsmittel gelöst werden. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen

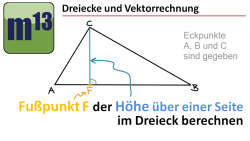
m13v0437 Drei Punkte eines Dreiecks ABC sind geben. Nun soll man mit Hilfe der Vektorrechnung den Fußpunkt der Höhe über der Grundseite AB berechnen. Diese Aufgabe soll mit den Mitteln gelöst werden, die man zu Anfang der Vektorrechnung lernt, also: Vektorzüge bestimmen und Skalarprodukt anwenden. Über die Höhe und der Grundseite kann man dann z.B. den Flächeninhalt des Dreiecks bestimmen. | auf teilen

m13v0595 Dies ist eine typische Konstruktionsaufgabe aus dem Gebiet der Vektorrechnung: Du sollst eine Raute konstruieren, indem du zunächst ein gleichschenkliges Dreieck konstruiert, welches du dann über einen weiteren Punkt zur Raute ergänzt. Auch sollst du wissen, wie man prüft, ob eine Raute ein Quadrat ist. Eine Aufgabe aus der Serie "So ähnlich im Abi gesehen". Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen

m13v0620 Drei Punkte sind gegeben, einer der Punkte enthält einen Parameter. Nun sollst du diese Punkte durch einen weiteren Punkt so ergänzen, dass man ein Rechteck erhält. Ahnst du schon, dass das Skalarprodukt hier ins Spiel kommt? Arbeitsblatt zum Download | auf teilen

m13v0641 Die Punkte A, B und C eines Dreiecks sind gegeben. Die x₁-Koordinate von A enthält einen Parameter k. Nun sollst du alle Werte von k bestimmen, so dass das Dreieck ABC rechtwinklig ist. Dies ist eine typische Aufgabe, bei der das Skalarprodukt zum Einsatz kommt. Arbeitsblatt zum Download | auf teilen

m13v0609 Drei Punktes eines Dreiecks sind gegeben, wobei einer der Punkte in Abhängigkeit eines Parameters angegeben ist. Jetzt sollst du zeigen, dass alle Dreiecke im Punkt A rechtwinklig sind. Außerdem sollst du den Parameter so bestimmen, dass das Dreieck zusätzlich auch gleichschenklig ist. Ein Video aus der Serie "So ähnlich im Abi gesehen". Arbeitsblatt zum Download | auf teilen

m13v0623 Bei dieser Aufgabe musst du einige Kompetenzen zusammenfügen: (1) Woran erkennt man, dass drei Punkte eine besondere Lage im Koordinatensystem haben? (2) Wie prüft man, ob ein rechtwinkliges Dreieck vorliegt? (3) In welchem Zusammenhang stehen Grundfläche und Volumen einer Pyramide? Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen

m13v0681 Ein Video zum Aufgabentyp „Beweise mit Vektoren“: Hier soll eine besondere Eigenschaft des gleichschenkligen Dreiecks bewiesen werden. Arbeitsblatt zum Download | auf teilen