m13v0178  In diesem Video werden die verschiedenen Methoden zum Lösen quadratischer Gleichungen gezeigt. Welche Methode man anwendet, hängt davon ab, in welcher Form die quadratische Gleichung gegeben ist und aus welchen Komponenten sie zusammengesetzt ist: Je nach Zusammensetzung spricht man von allgemeinen quadratischen Gleichungen, gemischt-quadratischen Gleichungen bzw. rein-quadratischen Gleichungen. Die unterschiedlichen Lösungsmethoden werden im Video vorgestellt. | auf  teilen

 m13v0179  In diesem Video werden drei Aufgabenbeispiele gezeigt, die am Ende drauf hinauslaufen, dass eine quadratische Gleichung zu lösen ist. Diese Aufgabenbeispiele sind: (1.) Schnittpunktbestimmung zweier Parabeln; (2.) Schnittpunktbestimmung einer Parabel mit einer Geraden und (3.) eine Textaufgabe, bei der man die Seitenlängen eines Rechtecks bestimmen soll, wenn man den Gesamtflächeninhalt kennt. Du siehst also, das Lösen von quadratischen Gleichungen ist eine wichtige Kompetenz, die man gut beherrschen soll.  | auf  teilen

 m13v0160  Immer ist der Graph einer quadratischen Funktion eine Parabel, und jede Parabel hat einen Scheitelpunkt. Man kann eine quadratische Funktion, welche in der allgemeinen Form angegeben ist, in die sogenannte Scheitelpunktform überführen, aus der man direkt die Koordinaten des Scheitelpunktes ablesen kann. Die zugrundeliegende Methode dieser Umformung ist die quadratische Ergänzung; wie diese funktioniert, wird in diesem Video behandelt. | auf  teilen

 m13v0116  Die pq-Formel zum Lösen von quadratischen Gleichungen gehört wohl zu den "berühmtesten" Formeln, die man in der Schule lernt. In diesem Video wird diese Formel hergeleitet. Die Herleitung erfolgt wieder über die Methode der quadratischen Ergänzung. | auf  teilen

 m13v0541  In dem Video m13v0116 hatten wir die pq-Formel als Lösungsformel zum Lösen quadratischer Gleichungen über die Methode der quadratischen Ergänzung hergeleitet. Zur Anwendung der pq-Formel muss die quadratische Gleichung in Normalform (x²+px+q=0) angegeben sein. In diesem Video leiten wir die sogenannte abc-Formel her, mit denen man quadratische Gleichungen lösen kann, die in der allgemeinen Form ax²+bx+c=0 angegeben sind. | auf  teilen

 m13v0766  Quadratische Gleichungen kann man zwar immer mit der pq-Formel oder Mitternachtsformel lösen, aber oft lassen sie sich schneller ? manchmal schon durch Hingucken ? lösen. Diese Aufgabe hilft dir, deinen Blick für "einfache" quadratische Gleichungen zu schärfen. | Arbeitsblatt zum Download | auf  teilen

 m13v0551  In dieser Lektion lernst du die sogenannte Nullstellenform der quadratischen Funktion kennen. Diese Form heißt so, weil man aus ihr direkt die Nullstellen des Funktionsgraphen entnehmen kann. Natürlich kann die Nullstellenform nur für solche quadratischen Funktionen angegeben werden, die tatsächlich auch reelle Nullstelle(n) besitzen.  | auf  teilen

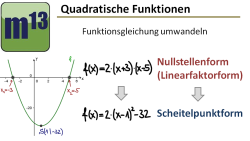
 m13v0559  In diesem Video wird gezeigt, wie man die Nullstellenform (Linearfaktorform) der quadratischen Funktion in die Scheitelpunktform umformt.  | auf  teilen

 m13v0246  In diesem Video lernst du, wie man quadratische Gleichungen zeichnerisch (und daher näherungsweise) lösen kann. Die Methode beruht darauf, dass man die Quadratische Gleichung zunächst so umformt, dass links nur der quadratische Term steht und rechts alles andere (dies ist dann entweder ein linearer oder konstanter Term). Dann zeichnet man die Funktionen links und rechts des Gleichheitszeichens separat ins Koordinatensystem, und falls sich die Graphen schneiden, liest man die x-Werte der Schnittpunkte ab - dies sind die Lösungen der Gleichung. Im Video wird dies Schritt für Schritt erklärt.  | auf  teilen

 m13v0588  Beim zeichnerischen Lösen von quadratischen Gleichungen wird die Gleichung so umgeformt, dass auf der rechten und linken Seite des Gleichheitszeichens Funktionen stehen, die man leicht ins Koordinatensystem einzeichnen kann. Die Schnittstellen sind dann die Lösungen. In diesem Video gibt es drei Übungsaufgaben und der ins Koordinatensystem eingezeichnete Graph der Normalparabel y=x2 ist vorgegeben ? den Rest musst du machen. | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf  teilen

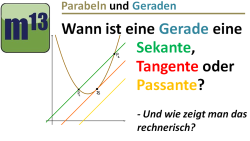
 m13v0113  In diesem Video geht es um die gegenseitige Lage zwischen Gerade und Parabel: Ist die Gerade eine Sekante, Tangente oder Passante - und wie untersucht man diese Möglichkeiten rechnerisch? | auf  teilen

 m13v0757  In dieser Aufgabe sind zwei quadratische Funktionen gegeben, wobei eine als Funktionenschar mit dem Parameter k definiert ist. Ziel ist es, den Wert von k so zu bestimmen, dass die beiden Parabeln genau einen Schnittpunkt haben. Tipp: Überlege, wie viele Lösungen die Schnittstellengleichung haben soll, und wie dabei die Berechnung der Diskriminante hilfreich sein kann. | Arbeitsblatt zum Download | auf  teilen

 m13v0758  Mit dieser Aufgabe kannst du dein Verständnis der Diskriminante als Werkzeug zur Analyse quadratischer Funktionsscharen vertiefen. Konkret sollst du die Diskriminante einer quadratischen Funktion in Abhängigkeit von einem Parameter bestimmen und dann mit dem Ergebnis nachweisen, dass die Graphen der Funktionsschar immer zwei Nullstellen besitzen. | Arbeitsblatt zum Download | auf  teilen

 m13v0780  Die Nullstellen einer quadratischen Funktion f(x)=ax²+bx+c lassen sich mit der Lösungsformel bestimmen. In dieser Aufgabe geht es speziell um den Koeffizienten b. Kannst du anhand der Diskriminante argumentieren, warum es einerseits immer möglich ist, einen Wert für b zu finden, sodass die Funktion zwei Nullstellen hat, es andererseits aber nicht immer möglich ist, einen Wert für b zu finden, sodass die Funktion eine doppelte Nullstelle hat? | Arbeitsblatt zum Download | auf  teilen

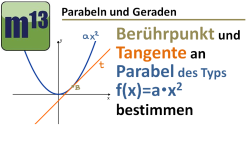
 m13v0324  Betrachtet wird eine Parabel des Typs f(x)=a·x². Wenn man eine allgemeine Gerade g(x)=mx+b hat, welche die Parabel nur in einem Punkt berührt, dann ist die Gerade ja eine Tangente (siehe dazu auch das Video m13v0113). Mit dieser Vorüberlegung über die Anzahl der Schnittpunkte von Parabel und Geraden soll nun eine allgemeine Tangentengleichung hergeleitet werden.
Beachte: In dieser Aufgabe werden nur die Methoden verwendet, die man am Anfang der Einführungsphase kennt (also ohne Differentialrechnung). | auf  teilen

 m13v0756  Dieses Video behandelt wichtige Grundaufgaben zu quadratischen Funktionen und Gleichungen. Du übst, wie man Punkte berechnet, die auf dem Funktionsgraphen liegen, und wie man die Schnittpunkte zwischen Parabel und Gerade ermittelt. | Arbeitsblatt zum Download | auf  teilen

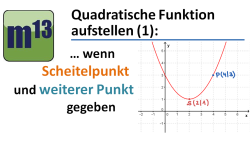
 m13v0235  In diesem Video lernst du, wie man eine Parabelgleichung (quadratische Gleichung) aufstellt, wenn man den Scheitelpunkt der Parabel und einen weiteren Punkt gegeben hat. Ausgangspunkt ist die Formulierung der Scheitelpunkt-Form; durch das Einsetzen der Koordinaten des weiteren Punktes bestimmt man die Streckungsfaktor. | auf  teilen

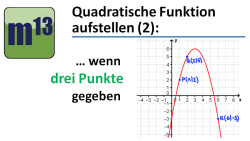
 m13v0236  In diesem Video lernst du, wie man eine Parabelgleichung (quadratische Gleichung) aufstellt, wenn man drei Punkte einer Parabel gegeben hat. Wesentlicher Schritt hierbei ist das Lösen eines linearen Gleichungssystems. | auf  teilen

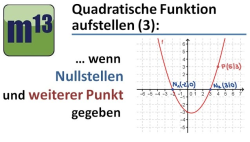
 m13v0237  In diesem Video lernst du, wie man eine Parabelgleichung (quadratische Gleichung) aufstellt, wenn man die Nullstellen der Parabel und einen weiteren Punkt der Parabel gegeben hat. Hier geht man von der sogenannten Nullstellenform der quadratischen Funktion aus und bestimmt dann den Strechungs- bzw. Stauchungsfaktor... | auf  teilen

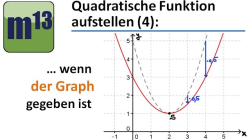
 m13v0245  In diesem Video lernst du, wie man eine Parabelgleichung (quadratische Gleichung) aufstellt, wenn man den Graphen der Parabel gegeben hat. Auch hier geht man von der Scheitelpunktform aus und guckt dann, wie die Parabel gegenüber der Normalparabel gesteckt oder gestaucht ist... | auf  teilen

 m13v0783  In dieser Aufgabe sollst du Beispiele für quadratische Funktionen aufstellen, die den geforderten Eigenschaften entsprechen. Dabei musst du dein Verständnis der verschiedenen Darstellungsformen quadratischer Funktionen (Scheitelpunktform, Nullstellenform, allgemeine Form) anwenden. Du entscheidest, welche Form du am besten wählst und wie du sie zielgerichtet einsetzt, um die Öffnungsrichtung, Nullstellen und den Scheitelpunkt der Parabel zu berücksichtigen. | Arbeitsblatt zum Download | auf  teilen

 m13v0555  In diesem Video geht es um den Satz von Vieta, der einen Bezug von p und q in der Gleichung x²+px+q=0 und den Lösungen der Gleichung herstellt (sofern es Lösungen gibt, versteht sich). Das Tolle am Satz von Vieta ist, dass man für einfache quadratische Gleichungen - mit ein bisschen Übung - direkt die Lösungen durch Hingucken bestimmen kann (ohne, dass man die pq-Formel anwenden muss). In dem Video wird zunächst der Satz von Vieta hergeleitet, danach werden drei Beispiele gezeigt. | auf  teilen

 m13v0553  Dies ist eine Übungsaufgabe, bei der der Satz von Vieta zum Einsatz kommt. Es ist nur eine von zwei Nullstellen der quadratischen Gleichung x²+px+q=0 angegeben und es ist jeweils nur der Wert von p oder q angegeben. Jetzt soll die komplette Funktionsglechung und die zweite Lösung ermittelt werden. | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf  teilen

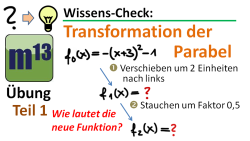
 m13v0249  Dieses Video ist ein Übungsvideo zur Transformation von Parabeln. Ausgehend von einer Parabelfunktion, die in Scheitelpunktform angegeben ist, soll man mehrere Transformationen hintereinander durchführen und jeweils die neue Gleichung aufstellen. | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf  teilen

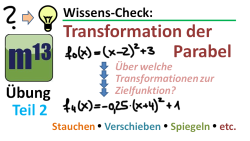
 m13v0250  Ein weiteres Übungsvideo zur Transformation von Parabeln. Diesmal ist die Ausgangs- und die Zielfunktion gegeben, und du sollst überlegen, über welche Transformationen man zur Zielfunktion gelangt. | Arbeitsblatt zum Download | auf  teilen

 m13v0768  Bei dieser Aufgabe musst du zwei Kompetenzen zusammenbringen: (1.) Überführe die quadratische Zielfunktion in die Scheitelpunktform, um anschließend (2.) die notwendigen Transformationsschritte zu bestimmen, die den Graphen der Normalparabel in den Graphen der Zielfunktion überführen. | Arbeitsblatt zum Download | auf  teilen

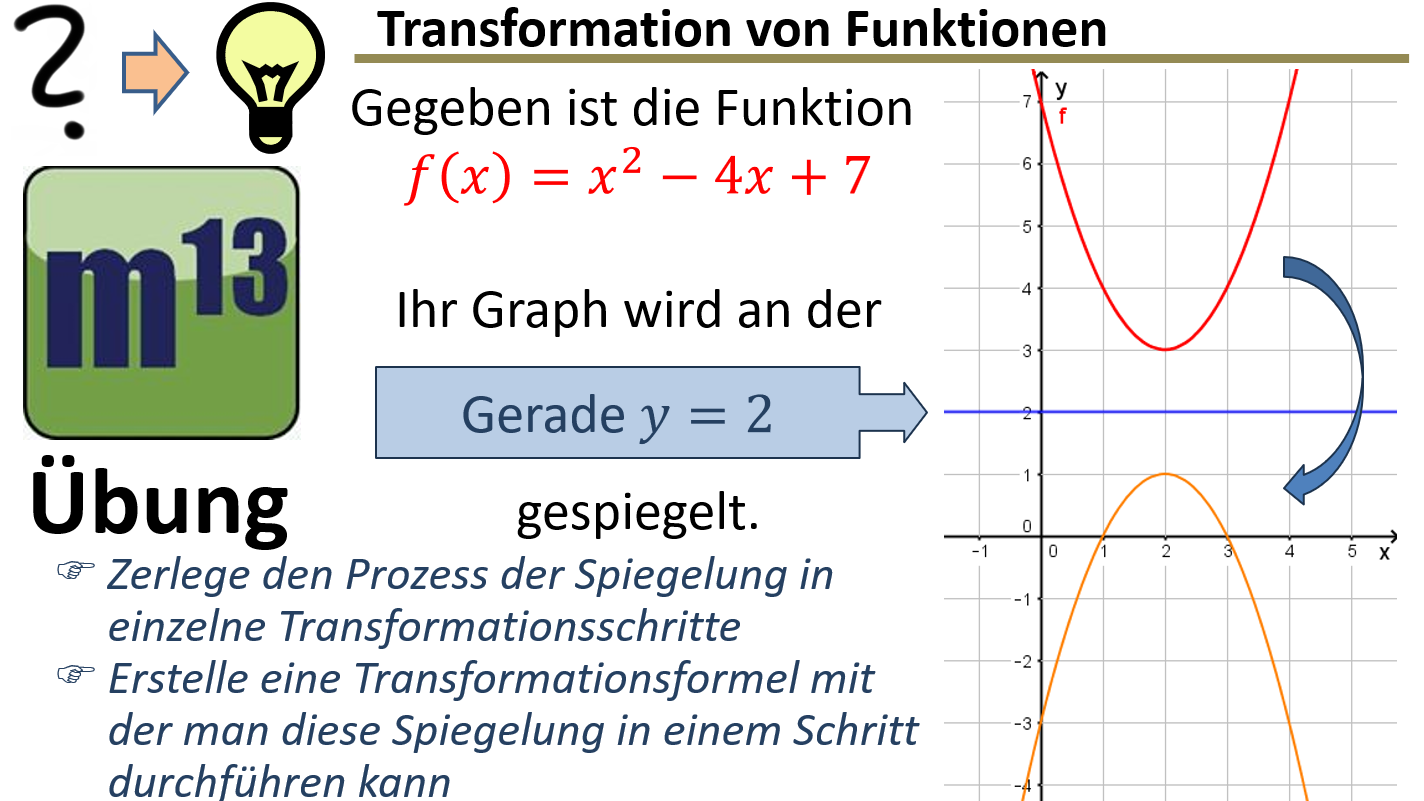
 m13v0755  Bei dieser Aufgabe sollst du schrittweise eine allgemeine Transformationsformel entwickeln, mit der man den Graphen einer Funktion an einer horizontalen Geraden spiegeln kann, die nicht die x-Achse ist. | Arbeitsblatt zum Download | auf  teilen