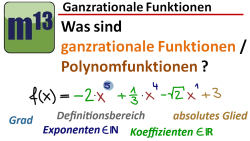
m13v0395 In diesem Einstiegsvideo wird erklärt, was ganzrationale Funktionen - auch Polynomfunktionen genannt - sind. Zuerst werden an einigen Beispielen die wesentlichen Merkmale von ganzrationalen Funktionen erklärt. Dabei wird ebenfalls erläutert, was man unter Koeffizienten und dem Grad einer ganzrationalen Funktion versteht. Nach den Beispielen wirst du dann sicherlich auch die allgemeine Definition für ganzrationale Funktionen verstehen. | auf teilen

m13v0397 Nachdem du im vorigen Video gelernt hast, was ganzrationale Funktionen sind, sollst du in diesem Übungsvideo entscheiden, ob eine gegebene Funktion eine ganzrationale Funktion ist oder nicht. Du wirst sehen, dass es knifflige Fälle gibt. Lass dich nicht hinters Licht führen... Arbeitsblatt zum Download | auf teilen

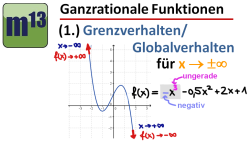
m13v0102 In diesem Video erfährst du, wie man bei ganzrationalen Funktionen (Polynomfunktionen) sehr einfach den Verlauf des Graphen bei x gegen plus oder minus unendlich herausfinden kann. | auf teilen

m13v0622 Wenn man eine ganzrationale Funktion hinsichtlich ihres Verhaltens für x→±∞ untersucht, muss man den Grad der Funktion und den Leitkoeffizienten betrachten. Dies ist eine Übung, bei der - neben den einfachen Fällen - auch ganzrationale Funktionen, die in faktorisierter Form gegeben sind, untersucht werden sollen. Eine klassische Klausuraufgabe. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen

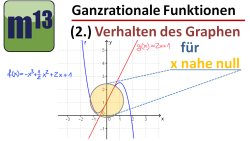
m13v0252 In diesem Video erfährst du, wie man bei ganzrationalen Funktionen (Polynomfunktionen) den Verlauf des Graphen in der Nähe der y-Achse, also für x-Werte nahe null, herausfinden kann. | auf teilen

m13v0403 In dieser Übung sollst du das Globalverhalten einer ganzrationalen Funktion bestimmen - und zwar nur durch Hingucken. Die Funktion ist dabei aber nicht immer in der "schönen" Summandenform angegeben, sondern als Produkt. Dennoch ist das eine einfache Aufgabe, da das Verhalten des Graphen für x gegen plus/minus unendlich ja nur vom Summanden mit der höchsten Potenz von x und dessen Koeffizienten abhängt. Dieser Summand kann aber ohne große Rechnung schnell ermittelt werden, auch wenn das Polynom in faktorisierter Form angegeben ist... Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen

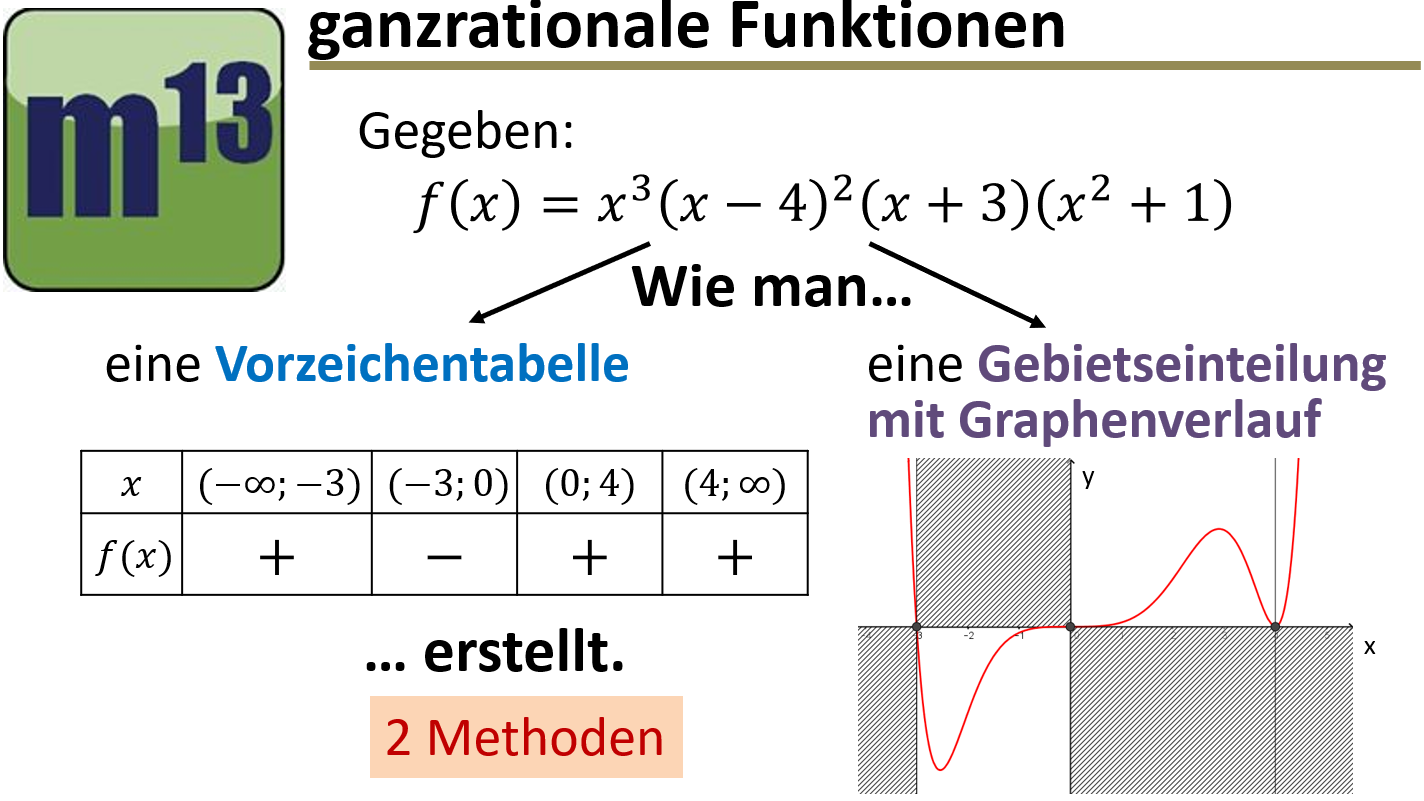
m13v0825 In diesem Video erfährst du, wie du für eine ganzrationale Funktion in faktorisierter Form eine Vorzeichentabelle erstellst und den Graphenverlauf durch eine Gebietseinteilung analysierst. Dabei lernst du zwei Methoden kennen: eine auf Testwerten basierte Strategie und eine, die das Globalverhalten der Funktion berücksichtigt. Arbeitsblatt zum Download | auf teilen

m13v0739 Bei dieser Übung sollst du untersuchen, wie sich Transformationen des Graphen der Funktion f auf das Globalverhalten, also das Verhalten der Funktionswerte für x→±∞, auswirkt. Arbeitsblatt zum Download | auf teilen

m13v0778 Wie müssen die Funktionsterme durch passende Werte des Parameters k angepasst werden, damit der Graph der Funktion Standardsymmetrie erlangt ? also entweder y-achsensymmetrisch oder punktsymmetrisch zum Ursprung wird? Arbeitsblatt zum Download | auf teilen

m13v0394 In diesen Übungsaufgaben sollst du die Punktsymmetrie eines Graphen einer ganzrationalen Funktion zu einem gegebenen Punkt nachweisen. Ein Lösungsansatz dabei ist, dass man sich überlegt, wie man den Graphen verschieben müsste, damit die Funktion punktsymmetrisch zum Ursprung wäre. Teil 2 mit einer verwandten Aufgaben hat die Aufruf-ID: m13v0393. Arbeitsblatt zum Download | auf teilen

m13v0393 In dieser Übung sollst die Achsensymmetrie eines Graphen einer ganzrationalen Funktion zu einer gegebenen senkrechten Geraden nachwiesen werden. Auch hier ist das Grundprinzip, dass man sich überlegt, wie man den Graphen verschieben müsste, damit die Funktion achsensymmetrisch zur y-Achse wäre. Siehe auch Teil 1 mit der Aufruf-ID: m13v0394. Arbeitsblatt zum Download | auf teilen

m13v0103 Dieses Video gibt eine allgemeine Übersicht über die verschiedenen Methoden der Nullstellenbestimmung ganzrationaler Funktionen vom Grad 3 und höher. | auf teilen

m13v0169 Wenn eine ganzrationale Funktion in faktorisierter Form angegeben ist oder sich durch Ausklammern der Variablen leicht faktorisieren läßt, dann ist die Nullstellenberechung sehr einfach durchzuführen. In diesem Video wird gezeigt, was die faktorisierte Form so attraktiv macht. | auf teilen

m13v0105 In diesem Video wird gezeigt, wie man sogenannte biquadratische Gleichungen löst bzw. die Nullstellen von biquadratischen Gleichungen bestimmt. Dies ist eine von mehreren Methoden zur Nullstellenbestimmung von ganzrationalen Funktionen vom Grad 3 und höher. Die anderen Videos dieser Serie sind unten gelistet. | auf teilen

m13v0170 In diesem Video wird gezeigt, wie man mit Hilfe der Polynomdivision eine ganzrationale Funktion faktorisiert. Dies ist eine wichtige Methode zur Nullstellenbestimmung von ganzrationalen Funktionen (Polynomen) vom Grad 3 und höher. Durch die Faktorisierung zerlegt man das Ausgangspolynom in einfachere Polynom-Faktoren niedrigeren Grades, deren Nullstellen dann einfacher bestimmt werden können. | auf teilen

m13v0104 Dies ist ein Ergänzungsvideo zum Grundlagenvideo zur Polynomdivision. Hier werden weitere Beispiele vorgemacht und es wird erklärt, worauf man beim Durchführen einer Polynomdivision zu achten hat, wenn das Polynom nicht alle Potenzen von x in absteigender Reihe enthält. | auf teilen

m13v0656 Dies ist eine klausurtypische Aufgabe zur Untersuchung einer ganzrationalen Funktion, die verschiedene Grundkompetenzen abdeckt, wie z.B. (a.) Umwandeln der faktorisierten Funktion in die allgemeine Form, (b.) Untersuchung des Verhaltens für x→±∞, (c.) Untersuchung der Symmetrie des Grpahen, (d.) Nullstellenbestimmung und (e.) Anfertigen einer Skizze. Arbeitsblatt zum Download | auf teilen

m13v0592 Bei dieser Übung, soll ein Parameter in einer Polynomfunktion so bestimmt werden, dass die Polynomdivision durch einen gegebenen Linearfaktor ohne Rest aufgeht. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen

m13v0660 Dies ist eine Art Steckbriefaufgabe: Von einem Polynom sind zwei Linearfaktoren bekannt und du sollst die fehlenden Koeffizienten in der Funktionsgleichung ermitteln... Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen

m13v0736 Bei dieser Aufgabe ist eine ganzrationale Funktion zum Teil in faktorisierter Form angegeben. Es kommt jedoch auch ein linearer Summand vor. Das Ziel ist es, die Funktionsgleichung als vollständige Linearfaktorzerlegung darzustellen und anschließend den Graphen der Funktion zu skizzieren. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen

m13v0171 Damit man eine Polynomdivision durchführen kann, muss eine Nullstelle des Polynoms bekannt sein. Wenn diese nicht angegeben ist, muss man eine Nullstelle "durch Raten" finden. In diesem Video wird gezeigt, wie man *gezielt* Nullstellen-Kandidaten für ganzrationaler Funktionen finden kann. | auf teilen

m13v0802 In dieser Aufgabe geht es darum, wie die Vielfachheit von Nullstellen den Verlauf des Graphen einer ganzrationalen Funktion beeinflusst. Ausgehend von drei vorgegebenen Nullstellen sollst du Funktionen unterschiedlichen Grades erstellen, wobei du zusätzliche vorgegebene Eigenschaften berücksichtigen musst. Arbeitsblatt zum Download | auf teilen

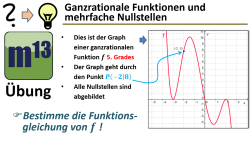
m13v0653 Eine Aufgabe zur Aufstellung eines Funktionsterms einer ganzrationalen Funktion durch Auswertung des Funktionsgraphen. Welche Informationen kannst du aus der Betrachtung der Nullstellen erschließen? Wie verwendest du den angegebenen Punkt, der auf dem Graphen liegt? Arbeitsblatt zum Download | auf teilen

m13v0751 Eine Art Steckbriefaufgabe: Gegeben ist der Graph einer ganzrationalen Funktion, und du sollst die Koeffizienten ihres Funktionsterms vom Typ f(x)=x³+bx²+cx+d bestimmen. Arbeitsblatt zum Download | auf teilen

m13v0799 Arbeitsblatt zum Download | auf teilen

m13v0582 Es soll ja vorkommen, dass eine ganzrationale Funktion an einer Stelle - nennen wir sie x₀ - mehrfache Nullstellen haben kann. Die Berechnung von f(x₀) liefert natürlich null als Ergebnis, doch ist es eine einfache oder mehrfache Nullstelle? In diesem Video erfährst du, wie du dies mit Hilfe der Polynomdivision untersuchen kannst. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen