Gebrochen-rationale Funktionen


m13v0569 In diesem Einstiegsvideo zu den gebrochen-rationalen Funktionen wirst du lernen: (1.) Was gebrochen-rationale Funktionen sind, (2.) wie und warum man echt und unecht gebrochen-rationale Funktionen unterscheidet und (3.) dass gebrochen-rationale Funktionen in verschiedenen Darstellungsformen angegeben werden können (wobei die eine oder die andere Form manchmal besser für die Funktionsuntersuchung sein kann). | auf teilen


m13v0772 In dieser Übungsaufgabe sollst du entscheiden, ob eine gegebene Funktion ganzrational oder gebrochenrational ist. Alle Funktionsterme sind als Bruchfunktionen auf jeden Fall rationale Funktionen ? aber Achtung: Nicht alle erfüllen die Anforderungen einer ganzrationalen Funktion! Finde heraus, welche Terme tatsächlich ganzrational und welche gebrochenrational sind. Arbeitsblatt zum Download | auf teilen
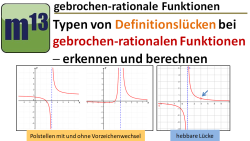

m13v0614 In diesem zweiten Teil der Lektionsserie über gebrochen-rationale Funktionen sprechen wir über Definitionslücken. Dort wo die Nennerfunktion Nullstellen hat, ist die Funktion nicht definiert und es gibt eine Definitionslücke. Du wirst lernen, dass Definitionslücken in verschiedener Form in Erscheinung treten können: als Polstellen mit senkrechter Asymptote und als hebbare Lücken. Wie man das alles, rechnerisch untersuchen kann, wird ausführlich vorgemacht. | auf teilen


m13v0615 In diesem Video werden wir uns mit dem Verhalten von gebrochen-rationalen Funktionen für x?±? beschäftigen. Dabei werden wir sehen, dass - in Abhängigkeit vom Grad des Zähler- und Nennerpolynoms - verschiedene Fälle auftreten können, nämlich, dass: (1) die x-Achse eine waagerechte Asymptote sein kann, (2) eine andere konstante Funktion als waagerechte Asymptote fungieren kann, (3) dass es aber auch eine lineare Funktion als schiefe Asymptote geben kann oder (4) krummlinige Funktionen als Näherungsfunktion auftreten können. Wie man das alles untersucht, wird ausführlich an Beispielen vorgemacht. | auf teilen


m13v0573 Bei dieser Übungsaufgabe hast du drei, sehr ähnlich aussehende gebrochen-rationale Funktionen gegeben, und du sollst den Definitionsbereich bestimmen und dann untersuchen, ob Definitionslücken als Polstellen oder hebbare Lücken auftreten. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
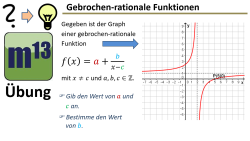

m13v0762 Du hast den Graphen einer gebrochen-rationalen Funktion vorliegen, aus dem du Asymptoten und Achsenschnittpunkte ablesen kannst. Deine Aufgabe ist es, die dazugehörige Funktionsgleichung aufzustellen. Arbeitsblatt zum Download | auf teilen


m13v0665 Die ist ein beliebter Aufgabentyp: du sollst mögliche Funktionsterme für gebrochen-rationale Funktionen aufstellen, die vorgegebene Asymptoten haben. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0763 Bei dieser Aufgabe geht es darum, gebrochen-rationale Funktionen anhand gegebener Eigenschaften zu konstruieren. Dabei musst du mehrere Aspekte beachten: (1) den Einfluss des Definitionsbereichs auf das Vorliegen von Polstellen, (2) die Bedingungen, die festlegen, ob es sich um eine Polstelle mit oder ohne Vorzeichenwechsel handelt, (3) wann waagerechte Asymptoten entstehen und (4) wodurch die Nullstellen einer gebrochen-rationalen Funktion festgelegt werden. Arbeitsblatt zum Download | auf teilen


m13v0575 Bei diesem Video aus der Serie "So ähnlich im Abi gesehen" ist eine Beschreibung von Funktionseigenschaften einer gebrochen-rationalen Funktion gegeben. Nun sollst du aus einer Auswahl von Ansätzen für die Funktionsgleichung - begründet! - den korrekten Ansatz identifizieren und schließlich die vollständige Funktionsgleichung aufstellen. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
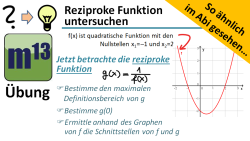

m13v0579 Gegeben ist der Graph einer Funktion f mit ihren Nullstellen. Jetzt sollst du Aussagen über die reziproke Funktion g(x)=1/f(x) machen, und zwar: hinsichtlich des Definitionsbereichs von g und zu Schnittstellen von f und g. Eine Aufgabe aus der Serie "So ähnlich im Abi gesehen" Arbeitsblatt zum Download | auf teilen
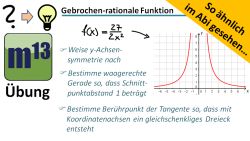

m13v0605 In diesem Video aus der Serie "So ähnlich im Abi gesehen" sollst du eine gebrochen-rationale Funktion untersuchen. Es geht um Nachweis einer y-Achsensymmetrie, die Bestimmung bestimmter Schnittpunkte mit einer waagerechten Gerade und um die Bestimmung der Tangente an den Graphen, so dass ein gleichschenkliges Dreieck mit den Koordinatenachsen entsteht. Arbeitsblatt zum Download | auf teilen
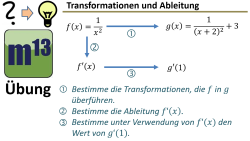

m13v0754 In dieser Aufgabe untersuchst du den Einfluss von Transformationen einer Funktion auf deren Ableitung. Dabei startest du mit einer einfachen Ausgangsfunktion, die du schrittweise transformierst. Statt die Ableitung der transformierten Funktion direkt zu berechnen, leitest du die Ausgangsfunktion ab und analysierst anschließend, wie sich die Transformationen auf die Ableitung auswirken. Arbeitsblatt zum Download | auf teilen


m13v0633 Bei dieser Aufgabe musst du deine Kenntnisse über gebrochen-rationale Funktionen, ihre Definitionslücken und Asymptoten zusammenbringen, und zwar auch im Kontext einer Funktionenschar ... Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0743 In diesem Video aus der Serie "So ähnlich im Abi gesehen" sollst du eine gebrochen-rationale Funktion untersuchen (Definitionslücken, Polstellen, hebbare Lücken, Asymptoten) und den Graphen der Funktion skizzieren. Eine hilfreiche Unterstützung bei dieser Aufgabe bietet die Tatsache, dass die Funktion in verschiedenen Darstellungsformen angegeben ist. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen