m13v0785 Bei dieser Aufgabe erstellst du 'neue' Funktionen aus 'alten', indem du die Ausgangsfunktionen durch verschiedene Rechenoperationen verknüpfst oder durch Verkettung, bei der eine Funktion in die andere eingesetzt wird. Diese Neuschaffung von Funktionen kann den Definitionsbereich verändern, was du ebenfalls untersuchen sollst. Arbeitsblatt zum Download | auf teilen

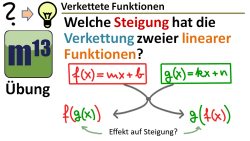
m13v0476 In diesem Übungsvideo betrachten wir die Verkettung zweier linearer Funktionen. Du sollst bestimmen, welche Steigung der Graph solch einer verketteten Funktion hat; dabei sind die beiden möglichen Richtungen der Verkettung zu berücksichtigen. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen

m13v0812 Bei dieser Aufgabe sind zwei Funktionen gegeben, von denen eine einen Parameter enthält. Deine Aufgabe ist es, zu untersuchen, für welchen Wert des Parameters die Verkettung der Funktionen in beide Richtungen zur gleichen Funktion führt. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen

m13v0786 In dieser mehrteiligen, klausurtypischen Aufgabe wird die verkettete Funktion f(x)=u(v(x)) analysiert, wobei die Graphen der Funktionen u(x) und v(x) gegeben sind. Gefordert sind Kompetenzen wie das Berechnen von Funktionswerten, das Ableiten von Funktionstermen aus den Graphen und das Untersuchen, wie die innere Funktion v(x) die Eigenschaften der verketteten Funktion beeinflusst. Arbeitsblatt zum Download | auf teilen

m13v0814 Dies ist eine klausurtypische Aufgabe zu verketteten Funktionen, bei der verschiedene Kompetenzen abgefragt werden. (1.) Verkettung in zwei Richtungen bestimmen, (2.) Ableiten mit der Kettenregel, (3.) Untersuchung der verketteten Funktionen und (4.) Aufstellen einer Tangentengleichung. Arbeitsblatt zum Download | auf teilen

m13v0530 Hier wird gezeigt, warum die Nullstellenbestimmung bei Funktionen des Typs f(x)=(ganzrationale Funktion)·(e-Funktion) relativ einfach ist. Antwort: weil der e-Funktionsfaktor selber keine Nullstellen hat. Die Nullstellen der zusammengesetzten Funktion sind also die Nullstellen der ganzrationalen Funktion, die als Faktor in der Funktion auftritt. Hier wird am Beispiel die Nullstellenbestimmung solcher zusammengesetzen Funktionen vorgemacht. | auf teilen

m13v0585 Die Bestimmung der Nullstellen einer zusammengesetzten Funktion des Typs f(x)=(ganzrationale Funktion)·(e-Funktion) ist sehr einfach, ja das kann sogar so einfach sein, dass man die Nullstellen im Kopf bestimmen kann. Ist dir klar, warum es in der Regel einfach ist? - Ein Video aus der Serie "Mathematisches Schnellkrafttraining". Arbeitsblatt zum Download | auf teilen

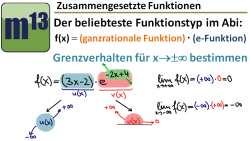
m13v0531 In diesem Video betrachten wir nun, wie man das Grenzverhalten für x→±∞ für die Funktion des Typs f(x)=(ganzrationale Funktion)·(e-Funktion) untersucht. Dazu schaut man sich das Grenzverhalten der einzelnen Faktoren an und berücksichtigt − falls erforderlich −, dass das Grenzverhalten einer e-Funktion über das einer ganzrationalen Funktion dominiert. | auf teilen

m13v0533 Dieses Video behandelt den Schritt, der nach dem Ableiten unserer Funktion des Typs f(x)=(ganzrationale Funktion)·(e-Funktion) folgen sollte, bei dem aber gerne mal Fehler gemacht werden: gemeint ist das Ausklammern, um die Ableitung − welche man nach Anwendung der Produktregel erhalten hat − in die faktorisierte Form zu überführen... | auf teilen

m13v0535 In diesem Video wird eine Formel für das schnelle Ableiten von Funktionen des Typs f(x)=(ganzrat. Funktion)·(e-Funktion) hergeleitet. Diese Formel liefert direkt die faktorisierte Form der Ableitung, die man ja z.B. zur Bestimmung von Extremstellen benötigt. | auf teilen

m13v0683 Für eine Reihe von zusammengesetzten e-Funktionen sollen Funktionseigenschaften ermittelt werden, die man schon durch "bloßes Hinschauen" erkennen kann. Arbeitsblatt zum Download | auf teilen

m13v0709 Dies ist eine weitere Übungsaufgabe zur Grenzwertuntersuchung von zusammengesetzten e-Funktionen. Bei Vorliegen einer waagerechten Asymptoten wird auch die Art der Annäherung (von oben oder unten) untersucht. Arbeitsblatt zum Download | auf teilen

m13v0570 Für eine zusammengesetzte Funktion f, die das Produkt aus ganzrationaler Funktion und e-Funktion ist, kann man sehr elegant eine Stammfunktion bestimmen, so wie es in diesem Video vorgemacht wird - dabei ähnelt die Vorgehensweise ein bisschen einer Steckbriefaufgabe. Hierbei wird keine Integrationsregel angewandt, sondern man nutzt die Eigenschaft der Stammfunktion F, dass F'(x)=f(x) ist, aus. Man benötigt einen (einfachen) Ansatz der Stammfunktion, dann ein bisschen Produktregel der Ableitung und schließlich Koeffizientenvergleich, und schon erhält erhältst du eine Stammfunktion... Arbeitsblatt zum Download | auf teilen

m13v0590 Dies ist Teil 1 der vollständigen Funktionsuntersuchung einer zusammengesetzten Funktion mit e-Funktion. Darin besprochen: (a.) Definitionsbereich, (b.) Symmetrie, (c.) Nullstellen, (d.) Verhalten an den Definitionsrändern. Zu dieser Aufgabe gibt es auch noch einen Teil 2 (m13v0591). Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen

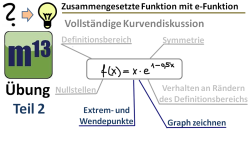
m13v0591 Dies ist Teil 2 der vollständigen Funktionsuntersuchung einer zusammengesetzten Funktion mit e-Funktion. Hier geht es weiter mit der Bestimmung der Extrem- und Wendepunkte, anschließend wird der Graph der Funktion anhand der ermittelten Informationen gezeichnet. Für Teil 1, siehe Video m13v0590. Arbeitsblatt zum Download | auf teilen

m13v0655 Dies ist eine Übungsaufgabe, bei der eine besondere Eigenschaft einer verketteten e-Funktion nachgewiesen werden soll. Arbeitsblatt zum Download | auf teilen

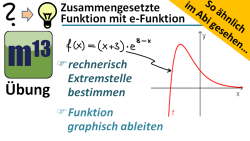
m13v0594 Für eine zusammengesetzte Funktion, die eine e-Funktion enthält, soll die Extremstelle bestimmt werden und durch graphisches Ableiten soll der Graph der Ableitungsfunktion ermittelt werden. Ein Video aus der Serie "So ähnlich im Abi gesehen". Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen

m13v0593 Weil die Integration des Funktionstyps f(x)=(ganzrationale Funktion)·(e-Funktion) über das Niveau des Grundkurses hinausgeht, man aber die Stammfunktion F für einige Standardaufgaben benötigt, wird häufig die Zwischenaufgabe "Zeige, dass F eine Stammfunktion von f ist" eingefügt. Dadurch sollst du zum einen zeigen, dass du die Definition einer Stammfunktion kennst, und außerdem kannst du die angegebene Stammfunktion dann bei nachfolgenden Aufgaben verwenden. Das Video zeigt dies im Kontext einer Beispielaufgabe... Arbeitsblatt zum Download | auf teilen

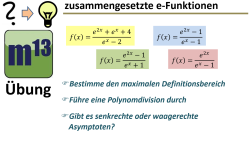
m13v0711 Bei mit e-Funktionen zusammengesetzten Funktionen, die als Bruchfunktionen auftreten, kann es Definitionslücken wie Polstellen und hebbare Lücken geben. Auch soll bei diesen Aufgaben das Grenzverhalten für x→±∞ und das Vorliegen horizontaler Asymptoten untersucht werden. Arbeitsblatt zum Download | auf teilen

m13v0721 In dieser Aufgabe geht es darum, den Graphen einer ganzrationalen Ausgangsfunktion f zu skizzieren und dabei die Vielfachheit der Nullstellen, den y-Achsenabschnitt und die Grenzwerte für x→±∞ zu berücksichtigen. Außerdem werden drei neue Funktionen als zusammengesetzte Funktionen von f betrachtet. Es wird erläutert, wie man den maximalen Definitionsbereich jeder Funktion bestimmt und welche Schritte dabei zu beachten sind. Arbeitsblatt zum Download | auf teilen