Einführung in die Vektorrechnung
Am Anfang der Vektorrechnung lernst du, wie man Punkte als Vektoren darstellt (Ortsvektoren) und wie man durch Addieren, Subtrahieren und Vervielfachung von Vektoren Vektorz?ge beschreiben kann, mit denen man Punkte in geometrischen Figuren und K?rpern bestimmen kann. Die ersten Videos enthalten einfache ?bungsaufgaben, die immer gerne im hilfsmittelfreien Teil der ersten Klausuren zum Thema genommen werden.

m13v0859 In dieser Aufgabe trainierst du den Umgang mit Vektoren und Punktverschiebungen im Koordinatensystem. Du konstruierst zu gegebenen Punkten neue Punkte so, dass ein bestimmter Verschiebungsvektor erfüllt ist. Dabei übst du das Zeichnen und Interpretieren von Vektoren und vertiefst das Verständnis von Vektoraddition und -subtraktion. Arbeitsblatt zum Download | auf teilen


m13v0860 In dieser Aufgabe vertiefst du den Umgang mit Vektoren, indem du die gesuchten Punkte rechnerisch bestimmst. Du berechnest zu gegebenen Punkten neue Punkte so, dass ein vorgegebener Verschiebungsvektor erfüllt ist, und trainierst dabei Vektoraddition und -subtraktion. Dieses Video ist das rechnerische Pendant zu Video m13v0859, das den zeichnerischen Zugang behandelt. Arbeitsblatt zum Download | auf teilen


m13v0337 Vektoren können eine Verschiebung darstellen, die man auf einen Punkt anwendet. Dadurch wird ein neuer Punkt festgelegt. In dieser Übungsaufgabe geht es darum, den resultierenden Punkt zu bestimmen. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
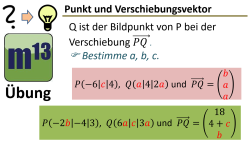

m13v0724 Bei dieser Aufgabe geht es um die Anwendung eines Verschiebungsvektors auf einen Punkt. Durch das Aufstellen einer geeigneten Vektorgleichung sollen die in den Vektoren vorkommenden Variablen bestimmt werden. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
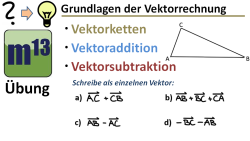

m13v0459 Bei dieser Übung sollst du im Dreieck ABC geeignete Richtungsvektoren entlang der Dreieckseiten einzeichnen, um mithilfe von Vektoraddition und -subtraktion den gegebenen vektoriellen Rechenausdrucks zu berechnen und als einzelnen Vektor darzustellen. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0646 Bei dieser Aufgabe sind für die Punkte A, B und C Verbindungsvektoren gegeben, die in Form einer Vektoraddition bzw. -subtraktion zu einer Termkette verbunden sind. Du sollst nun diesen Berechnungsterm so weit wie möglich vereinfachen... Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0661 Bei dieser Aufgabe geht es darum, Vektoren "schön" zu machen. Schön bedeutet, dass man Brüche oder Zahlen als Faktor vor den Vektor schreibt, wobei im Vektor dann nur möglichst kleine ganzzahlige Koordinaten stehen. Arbeitsblatt zum Download | auf teilen
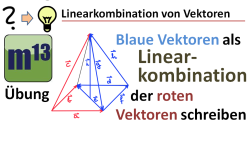

m13v0407 Bei dieser klassischen Übungsaufgabe sollen Kantenvektoren einer Pyramide als Linearkombination von drei vorgegebenen Vektoren geschrieben werden. Im Video wird gezeigt, wie man einen geschlossenen Vektorzug vom Anfang des gesuchten Vektors bis zu dessen Spitze konstruiert. Wichtig ist, dass man für diesen Vektorzug letztlich nur Vektoren verwendet, die man als Ausgangsvektoren gegeben hat. Im Video wird gezeigt wie es geht... Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0848 Bei dieser Aufgabe sollst du zunächst nachweisen, dass drei gegebene Punkte auf einer Geraden liegen. Anschließend sollst du bestimmen, in welchem Verhältnis der zwischenliegende Punkt die Strecke zwischen den beiden äußeren Punkten teilt. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
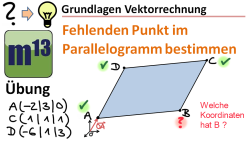

m13v0336 Drei Punkte (die nicht auf einer Geraden liegen) spannen bekanntermaßen ein Dreieck auf. Man kann aber auch einen vierten Punkt anfügen, so dass ein Parallelogramm entsteht. Um die Bestimmung dieses vierten Punktes geht es in diesem Video. Ein Klassiker in vielen Klausuren. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
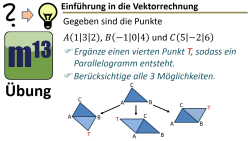

m13v0732 Dies ist eine typische Aufgabe, die am Anfang der Vektorrechnung immer gerne auch in Klausuren gestellt wird: Es sollen alle möglichen Punkte gefunden werden, mit denen sich ein Dreieck zu einem Parallelogramm ergänzen lassen. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
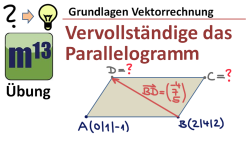

m13v0363 Auch hier geht es darum, fehlende Punkte in einem Parallelogramm zu bestimmen. Und wieder muss man, ausgehend von einem bekannten Punkt, versuchen mit einem geeigneten Vektorzug zu dem fehlenden Punkt zu gelangen. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0840 Bei dieser Aufgabe sollst du die fehlenden Eckpunkte eines Trapezes bestimmen. Dafür nutzt du die Koordinaten zweier gegebener Eckpunkte, den Mittelpunkt einer Diagonalen und die lineare Abhängigkeit der parallelen Seiten. Gefragt ist deine Fähigkeit, strategisch geeignete Vektorketten zu formulieren, um mit den vorhandenen Informationen die Ortsvektoren der gesuchten Punkte zu ermitteln. Arbeitsblatt zum Download | auf teilen


m13v0346 Ein Vektor ist ja Prinzip eine Länge und eine Richtung. In diesem Video erfährst du wie man die Länge des Vektors, man spricht dann auch vom Betrag des Vektors, berechnet. Am Anfang wird die Herleitung der Berechnungsformel für Vektoren im dreidimensionalen Raum erläutert (übrigens ein gern genommenes Referatthema), danach folgen Beispiele. | auf teilen
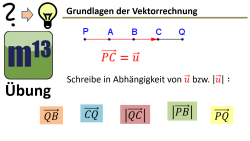

m13v0662 Dies ist eine Übungsaufgabe zur Beschreibung eines Vektors als Vielfaches eines anderen Vektors und darüber, wie Vielfache von Vektoren und ihre Vektorbeträge in Beziehung stehen. Arbeitsblatt zum Download | auf teilen
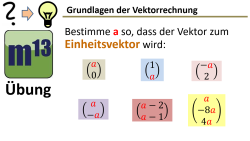

m13v0674 Bestimme den Parameter a so, dass ein Einheitsvektor entsteht. Geht das überhaupt immer? Arbeitsblatt zum Download | auf teilen
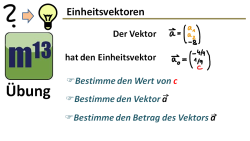

m13v0638 Bei dieser Aufgabe sollst du den Einheitsvektor zu einem gegebenen Vektor bestimmen, allerdings enthält der vorgegebene Vektor einige variable Parameter als Koordinaten, die das Problem interessanter machen... Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
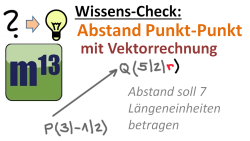

m13v0222 Eine Übungsaufgabe zur Bestimmung des Abstandes zweier Punkte mittels Vektorrechnung. In diesem Fall sollen die Koordinaten eines Punktes so gewählt werden, dass der Abstand der Punkte 7 Längeneinheiten beträgt. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
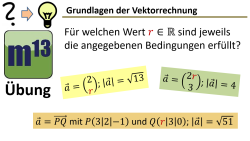

m13v0675 Ein häufig gesehener Aufgabentyp: Ein im Vektor vorkommender Parameter soll so bestimmt werden, dass der Vektor eine bestimmte Länge hat. Arbeitsblatt zum Download | auf teilen


m13v0473 Ein Video zur Koordinatengeometie: Zwei Punkte angegeben; bei einem der Punkte sind die Koordinaten in Abhängigkeit eines Parameters angegeben. Jetzt sollst du den Mindestabstand der Punkte ermitteln. Dies ist ein Video aus der Serie "So ähnlich im Abi gesehen" aus dem Themenkomplex Vektorrechnung. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0478 Bei dieser Übungsaufgabe sollst du den Abstand eines Punktes zu Koordinatenachsen, Koordinatenebenen und Koordinatenursprung bestimmen. Hier kommt es darauf an, dass du erkennst, welche Koordinateninformationen du auswählen musst, um den gesuchten Abstand über ein passendes rechtwinkliges Dreieck zu bestimmen... Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
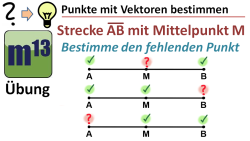

m13v0321 In diesem Video geht es um den Mittelpunkt einer Strecke zwischen zwei Punkten. Einmal sollst du den Mittelpunkt bestimmen, wenn die Koordinaten der äußeren Punkte angegeben sind; in anderen Aufgaben ist der Mittelpunkt und ein äußerer Punkt gegeben und man soll den fehlenden Punkt bestimmen. Arbeitsblatt zum Download | auf teilen
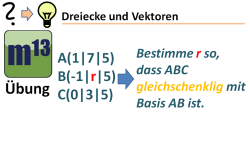

m13v0367 Drei Punkte bilden ja bekanntermaßen ein Dreieck (sofern sie nicht auf einer Geraden liegen). Hier enthält ein Punkt eine variable Koordinate. Nun soll bestimmt werden, für welchen Wert dieser Variable die drei Punkte ein gleichschenkliges Dreieck bilden. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
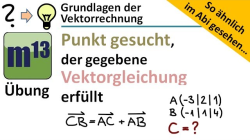

m13v0382 In dieser Übungsaufgabe soll ein Punkt berechnet werden, der eine gegebene Vektorgleichung erfüllt. Eine ähnliche Aufgabe kam im hilfsmittelfreien Teil einer Klausur des Landes Bayern dran. Hierbei geht es um grundlegende Kenntnisse der Vektorrechnung, d.h. Addition/Subtraktion von Vektoren, Umstellen von Vektorgleichungen und Berechnung des Ortsvektors eines Punktes. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
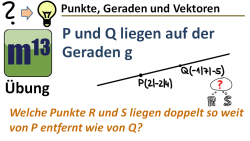

m13v0471 Zwei Punkte P und Q, die auf der Geraden g liegen, sind gegeben. Du sollst nun die Koordinaten zweier weiterer Geradenpunkte R und S bestimmen, die jeweils von P doppelt so weit entfernt sind wie von Q. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
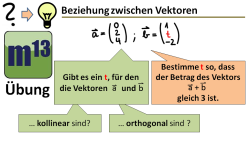

m13v0563 In diesem Übungsvideo sollst du die Beziehung zwischen zweier Vektoren hinsichtlich Kollinearität, Orthogonalität und dem Betrag untersuchen, und zwar in Abhängigkeit eines Parameters, der in einem der Vektoren als Parameter auftaucht. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
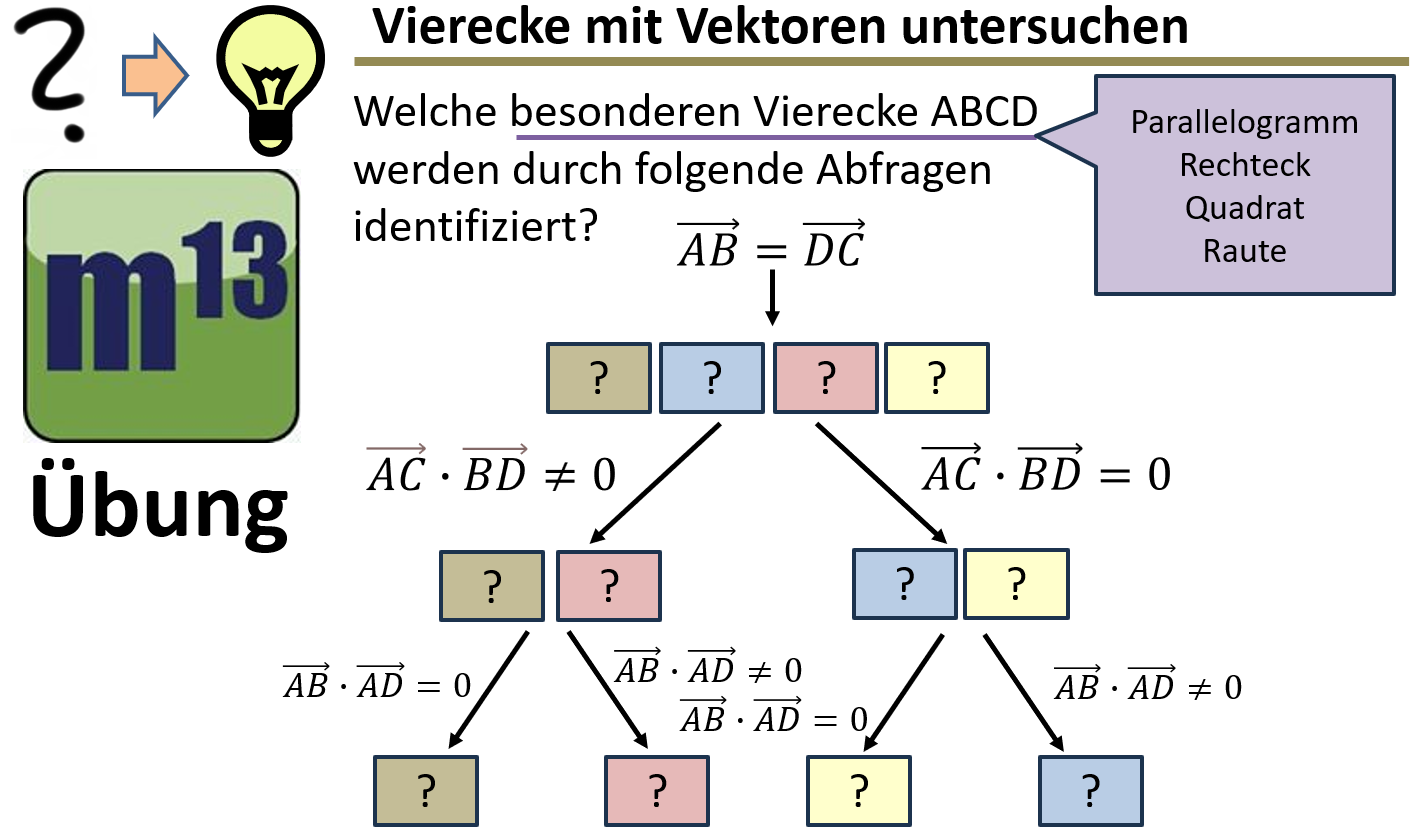

m13v0817 Du sollst besondere Vierecke mithilfe der Vektorrechnung identifizieren! Wir betrachten Parallelität, Orthogonalität und Länge von Seiten und Diagonalen, um herauszufinden, welche Vierecke in Frage kommen. Dabei folgen wir einer klaren Untersuchungsreihenfolge, die uns schrittweise zu immer weiteren Eingrenzungen führt, bis wir schließlich mit ausreichenden Bedingungen eine eindeutige Identifizierung erreichen. Arbeitsblatt zum Download | auf teilen
