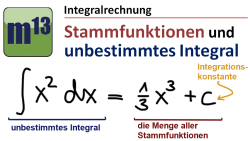
Integralrechnung
In diesem Kapitel werden wir in die Integralrechnung einsteigen. In einem späteren Kapitel werden wir uns weitere Anwendungen und die komplizierteren Integrationsregeln ansehen.Die einfachen Integrationsregeln
- Funktionen, die sich in die Potenzschreibweise umschreiben lassen. Dies beeinhaltet ganzrationale Funktionen, einfache Wurzelfunktionen und rationale Funktionen, in denen im Nenner eine Potenzfunktion steht
- Potenzfunktionen mit Exponent −1, deren Stammfunktion die ln-Funktion ist
- Funktionen mit linearer, verketteter Funktion


m13v0351 In diesem Video lernst du, wie man die Stammfunktion einer ganzrationalen Funktion bestimmt. Dabei wird summandenweise integriert: Potenzterme werden mit um 1 erhöhtem Exponenten und dem Kehrwert des neuen Exponenten aufgeleitet, konstante Faktoren bleiben erhalten. Wenn man die Menge aller Stammfunktionen bestimmen soll, so ergänzt man die Integrationskonstante +C, da es unendlich viele Stammfunktionen gibt. | auf teilen


m13v0767 Eine grundlegende Aufgabe: Überprüfe, ob die gegebene Funktion tatsächlich eine Stammfunktion der Ausgangsfunktion ist. Arbeitsblatt zum Download | auf teilen


m13v0811 In dieser Aufgabe geht es darum zu zeigen, dass eine gegebene Funktion F(x) eine Stammfunktion der Funktion f(x) ist. Dazu muss die Ableitung F'(x) gebildet und überprüft werden, ob sie mit f(x) übereinstimmt. Die Herausforderung liegt darin, dass diese Identität nicht immer direkt ersichtlich ist ? oft sind Umformungen nötig, um den Ausdruck in eine vergleichbare Form zu bringen. Arbeitsblatt zum Download | auf teilen
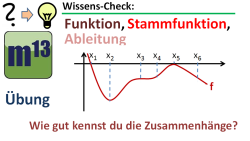

m13v0283 Bei dieser Übungsaufgabe sollst du zeigen, dass du die Zusammenhänge zwischen einer Funktion f, einer Stammfunktion F(x) und der Ableitung f'(x) verstanden hast. Der Graph der Funktion f ist gegeben. Welche Aussagen kann man über den Verlauf der Graphen von F(x) und f'(x) machen? Arbeitsblatt zum Download | auf teilen


m13v0765 Dies ist eine gute Aufgabe, mit der du dein Verständnis des Zusammenhangs zwischen einer Funktion, ihrer Ableitung und Stammfunktion prüfen kannst. Arbeitsblatt zum Download | auf teilen
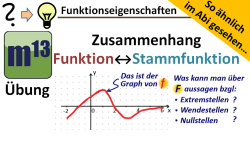

m13v0441 Bei dieser Aufgabe hat man den Graphen einer Funktion f gegeben und man soll überlegen, welche Aussagen man bezüglich einer Stammfunktion F von f im Hinblick auf Extremstellen, Wendestellen und Nullstellen machen kann. Dies ist ein sehr beliebter Aufgabentyp, der gerne im hilfsmittelfreien Teil von Klausuren zur Integralrechnung gestellt wird. Arbeitsblatt zum Download | auf teilen


m13v0477 In diesem Übungsvideo wird eine Stammfunktion F zu einer gegebenen Funktion f gesucht. Die Stammfunktion ist dabei so zu bestimmen, dass ihr Hochpunkt auf der x-Achse liegt. Für das Lösen der Aufgabe musst du einerseits die Aufleitungsregeln zur Bestimmung einer Stammfunktion als auch die Methoden der Funktionsuntersuchung beherrschen, denn du musst ja auch feststellen, an welcher Stelle die F einen Hochpunkt hat. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0734 Um diese Steckbriefaufgabe zu lösen, ist es erforderlich, dass du Kompetenzen aus der Kurvenuntersuchung und der Integralrechnung zusammenbringst. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0738 Hier folgt eine weitere Steckbriefaufgabe, die ihren Ausgang bei der zweiten Ableitung f'' nimmt. Anhand weiterer Informationen sollst du schließlich die Funktion f bestimmen. Eine ähnliche Aufgabe findest du bei m13v0734. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0457 Bei dieser Übungsaufgabe geht es darum, dass du den Zusammenhang zwischen Funktion und Stammfunktion auswertest, um diejenigen Stellen zu ermitteln, an denen Funktion und Stammfunktion parallele Tangenten haben. Dies ist ein Video aus der Serie "So ähnlich im Abi gesehen". Arbeitsblatt zum Download | auf teilen
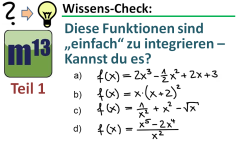

m13v0290 In diesem Übungsvideo geht es um die Bestimmung von Stammfunktionen von Funktionen, die auf den ersten Blick vielleicht etwas kompliziert aussehen, die aber tatsächlich mit den einfachen Integrationsregeln (Summenregel, Faktorregel, Potenzregel) integriert werden können. All diese Funktionen haben gemein, dass sie sich in die Potenzschreibweise umschreiben lassen, von der aus man die Funktion einfach aufleiten kann. Hierbei handelt es sich um ganz typische Klausuraufgaben. Arbeitsblatt zum Download | auf teilen
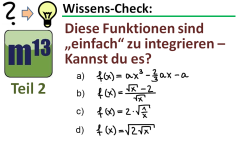

m13v0291 Dies ist das zweite Übungsvideo über "einfach integrierbare Funktionen" ? also solche Funktionen, die man mit den grundlegenden Integrationsregeln (Potenzregel, Summenregel, Faktorregel) aufleiten kann. Arbeitsblatt zum Download | auf teilen
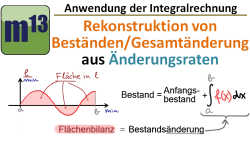

m13v0405 In diesem Video erfährst du, wie man mit Hilfe der Integralrechnung aus einer Funktion der Änderungsrate die Gesamtänderung eines Bestandes bestimmen kann. Wenn man eine Funktion hat, die die Änderungsrate einer Größe bestimmt (z.B. Meter PRO Sekunde, Liter PRO Minute, Anzahl Besucher PRO Stunde usw.), so liefert das Integral über diese Funktion die Gesamtänderung der Größe (also Meter, Liter, Anzahl), die in diesem Zeitraum erfolgt ist. Dies ist ein Einstiegsvideo, später sollen noch weitere Videos mit Übungsaufgaben folgen. Arbeitsblatt zum Download | auf teilen
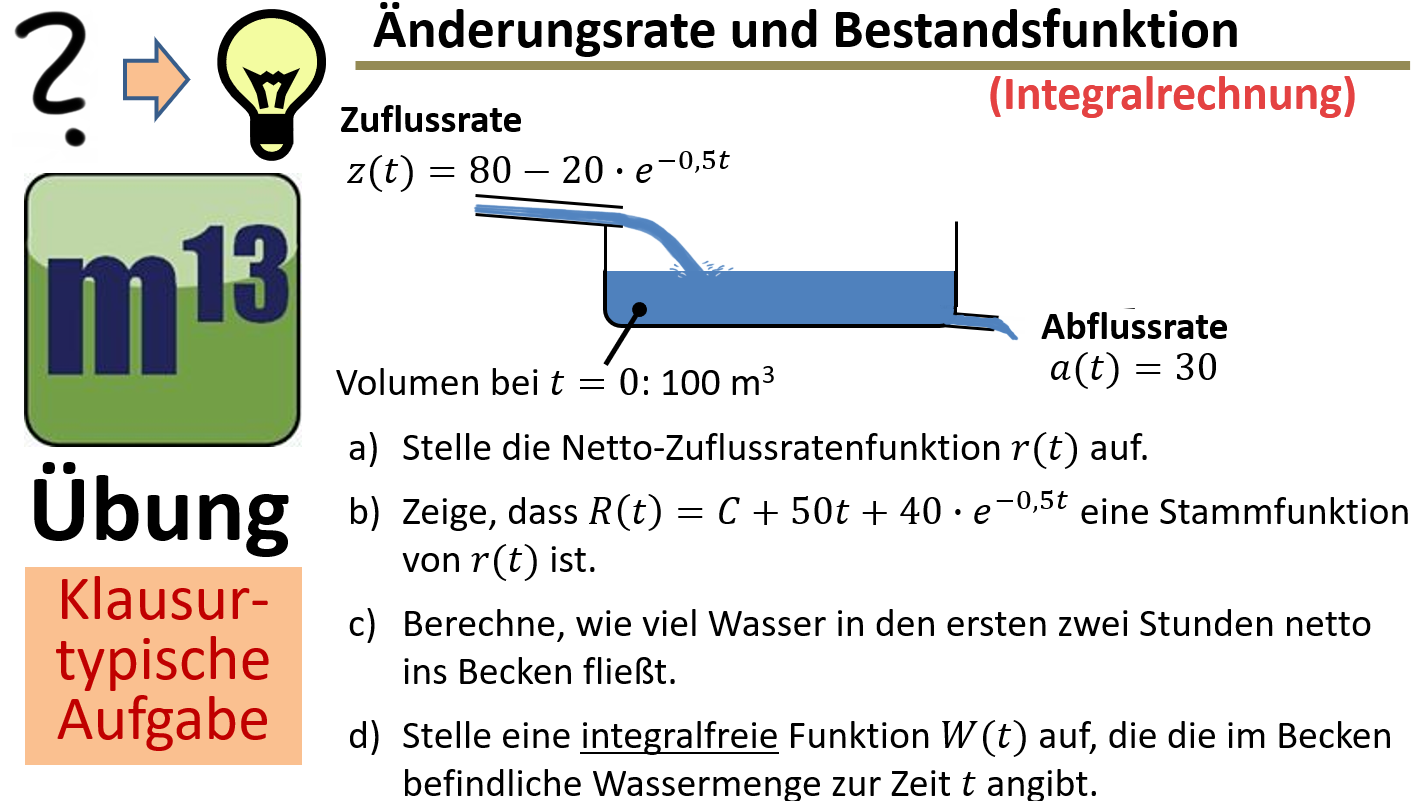

m13v0849 Bei dieser Aufgabe geht es um den Zusammenhang zwischen Änderungsrate und Bestandsänderung. Konkret sollst du aus einer gegebenen Nettozuflussrate von Wasser in ein Becken mithilfe eines bestimmten Integrals die insgesamt zugeflossene Wassermenge berechnet. Dabei wiederholst du das Bilden und Auswerten von Integralen, das Interpretieren von Funktionen in Sachzusammenhängen und das Verständnis von Bestand als aufintegrierter Änderungsrate. Arbeitsblatt zum Download | auf teilen
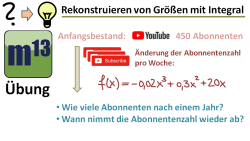

m13v0370 In diesem Video geht es um das Rekonstruieren einer Größe mithilfe von Integralen. Gegeben ist die Änderungsfunktion, welche die wöchentliche Zunahme/Abnahme der Abonnentenzahl eines Youtube-Kanals beschreibt; außerdem ist der Anfangsbestand gegeben. Jetzt soll mit Hilfe der Integralrechnung eine Bestandsfunktion bestimmt werden, mit der man die absolute Anzahl von Abonnenten in Abhängigkeit der Wochenzahl berechnen kann. Ausserdem soll man über die Änderungsratenfunktion eine Aussage machen, in welchem Zeitraum die Abonnentenzahl steigt und wann sie wieder fällt. Arbeitsblatt zum Download | auf teilen
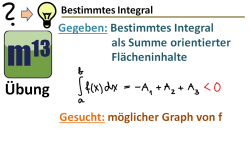

m13v0496 Dies ist ein Übungsvideo über den Zusammenhang zwischen dem Wert eines bestimmten Integrals und den über dem Integrationsintervall zwischen Graph und x-Achse eingeschlossenen Flächen. Hier soll man zwischen dem orientierten Flächeninhalt und dem absoluten Flächeninhalt unterscheiden. Arbeitsblatt zum Download | auf teilen
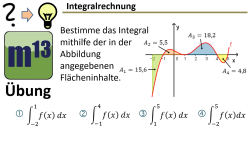

m13v0769 Bei dieser Aufgabe soll der Wert bestimmter Integrale berechnet werden, indem die Flächeninhalte, die der Graph mit der x-Achse einschließt, ausgewertet werden. Dabei ist es entscheidend, den sogenannten orientierten Flächeninhalt zu berücksichtigen, der unterscheidet, ob die eingeschlossene Fläche oberhalb oder unterhalb der x-Achse liegt. Arbeitsblatt zum Download | auf teilen
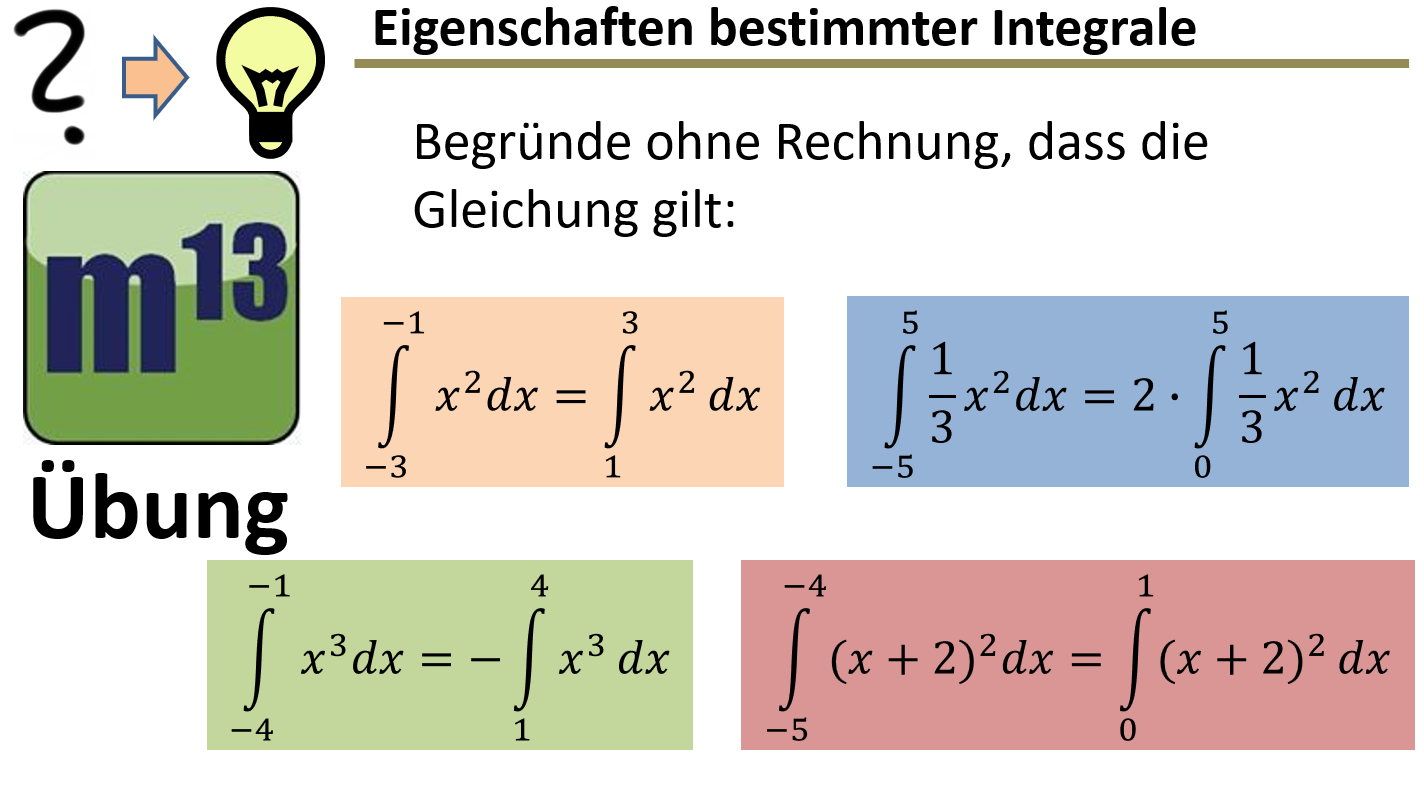

m13v0839 Bei dieser Aufgabe geht es darum, anhand der Eigenschaften der Integrandenfunktion und ihrer Symmetrieeigenschaften in Bezug auf die Integrationsgrenzen zu begründen, warum die gegebenen Integralgleichungen gelten. Dabei sollst du erkennen, wie Achsensymmetrie, Punktsymmetrie oder Verschiebungen der Funktion die Integrale beeinflussen. Arbeitsblatt zum Download | auf teilen
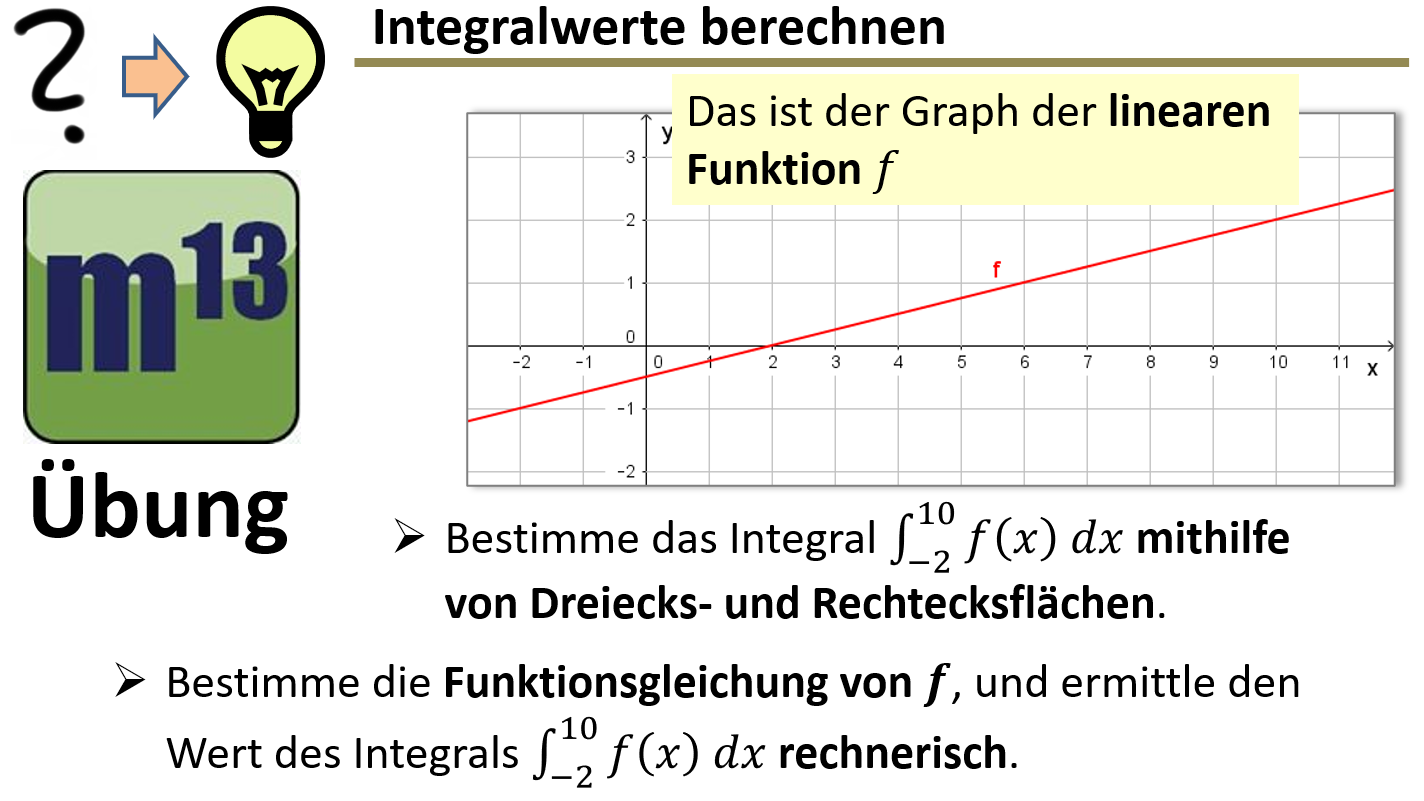

m13v0805 Wenn der Graph einer Funktion in einfache geometrische Figuren zerlegt werden kann, lässt sich die zwischen Graph und x-Achse eingeschlossene Fläche oft durch geometrische Berechnungen bestimmen. In dieser Aufgabe wendest du sowohl diese Methode als auch die Integration unter Anwendung des Hauptsatzes der Integralrechnung an. Arbeitsblatt zum Download | auf teilen
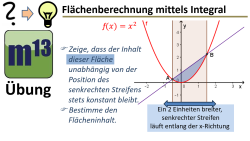

m13v0764 Eine spannende Aufgabe zur Flächenberechnung mittels Integralrechnung: Berechne die Fläche, die zwischen einer Sekante und dem Graphen einer Funktion eingeschlossen wird. Der Clou: Zeige, dass die Fläche ? egal wie das Intervall verschoben wird ? immer konstant bleibt. Arbeitsblatt zum Download | auf teilen
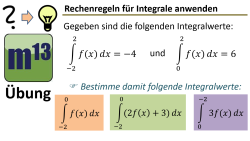

m13v0741 Bei dieser Aufgabe musst du zur Berechnung der Integralwerte die Rechenregeln für Integrale geschickt anwenden. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0499 Bei diesem Übungsvideo sind bestimmte Integrale von einfachen Funktionen gegeben. Du sollst nun abschätzen, ob der Integralwert größer, kleiner oder gleich Null ist. Dazu musst du dir überlegen, wie der Graph aussieht und wie sich die Flächen zwischen Graph und x-Achse über das betrachtete Intervall oberhalb und unterhalb der x-Achse verteilen. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0497 In diesem Übungsvideo geht es um die Berechnung des orientierten und des absoluten Flächeninhalts, den eine Funktion mit der x-Achse einschließt. Die Funktion ist in faktorisierter Form angeben (was die Aufgabe leichter machen sollte). Arbeitsblatt zum Download | auf teilen


m13v0498 In diesem Übungsvideo geht es um die Bestimmung der Gesamtfläche, die zwischen dem Graphen einer Funktion und der x-Achse auf einem angegebenen Intervall eingeschlossen wird. Das Besondere hier ist, dass es auf dem Intervall Nullstellen gibt, und man überlegen muss, ob man die Fläche mit einem bestimmen Integral "durchintegrieren" kann oder man das Intervall splitten muss und mehrere Integrale berechnen muss. Arbeitsblatt zum Download | auf teilen


m13v0830 In dieser Aufgabe geht es um die näherungsweise und exakte Bestimmung eines Integrals. Zunächst sollst du die von der Funktion und der x-Achse eingeschlossene Fläche geometrisch abschätzen und den orientierten Flächeninhalt bestimmen. Anschließend berechnest du das Integral exakt mithilfe des Hauptsatzes der Integralrechnung und vergleichst beide Werte. Arbeitsblatt zum Download | auf teilen


m13v0574 Bei dieser Aufgabe aus der Serie "So ähnlich im Abi gesehen" soll die obere Grenze eines bestimmten Integrals so bestimmt werden, dass sich der Integralwert Null ergibt. Das Ergebnis ist im Weiteren bei der Betrachtung der Beziehung zwischen dem Integralwert und dem orientiertem Flächeninhalt zwischen Graph und x-Achse wichtig. Arbeitsblatt zum Download | auf teilen
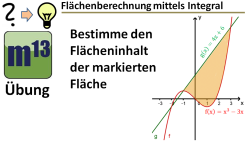

m13v0501 Bei dieser Übungsaufgabe soll die markierte Fläche berechnet werden, die von zwei Funktionsgraphen eingeschlossen wird. Die Schnittstellen können aus dem Schaubild abgelesen werden, sie sollen aber durch Rechnung bestätigt werden. Arbeitsblatt zum Download | auf teilen


m13v0795 Bei dieser Aufgabe geht es um die Berechnung der Fläche, die vom Funktionsgraphen, der Tangente an einem Berührpunkt und der x-Achse eingeschlossen wird. Dies ist eine mehrschrittige Aufgabe, bei der zunächst die Tangentengleichung bestimmt und anschließend ein passendes Berechnungsintegral aufgestellt werden muss. Arbeitsblatt zum Download | auf teilen
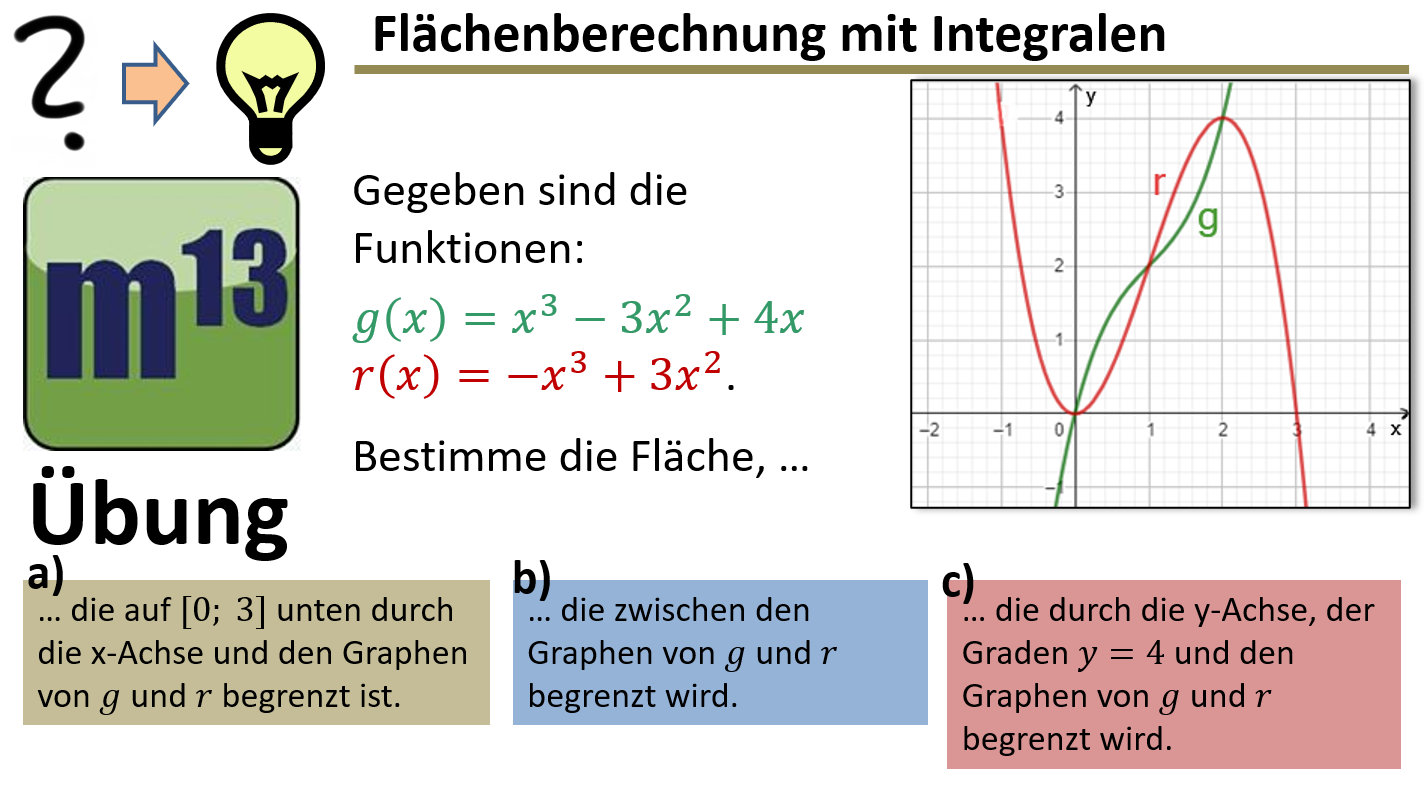

m13v0834 In dieser Aufgabe geht es darum, mithilfe von Integralen Flächen zu berechnen, die von zwei Funktionsgraphen, den Koordinatenachsen oder einer Geraden eingeschlossen werden. Entscheidend ist, dass du aus der Aufgabenstellung die jeweils gemeinte Fläche herausliest und eine passende Berechnungsstrategie entwickelst. Arbeitsblatt zum Download | auf teilen
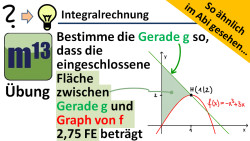

m13v0542 Eine Gerade geht durch den Hochpunkt der Funktion f. Jetzt ist genau diejenige Gerade g zu bestimmen, so dass die Fläche, die zwischen der Geraden g, der y-Achse und dem Graphen von f liegt, 2,75 Flächeneinheiten beträgt. Dies ist ein Video aus der Serie "So ähnlich im Abi gesehen". Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
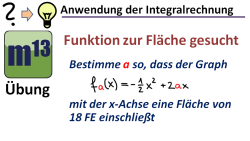

m13v0502 Bei dieser Aufgabe, soll ein Parameter einer Funktionenschar so bestimmt werden, dass der Graph mit der x-Achse eine vorgegebene Fläche einschließt. Arbeitsblatt zum Download | auf teilen
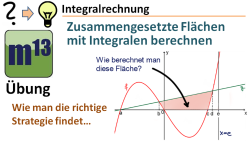

m13v0417 In diesem Video geht es darum, wie man strategisch vorgeht, um mit Integralen eine zusammengesetzte Fläche zu bestimmen. Diese Fläche kann zwischen Funktionsgraphen, Koordinatenachsen oder senkrechten Geraden eingeschlossen sein. Das Ziel ist, das Vorgehen zu lernen und den entsprechenden Rechenansatz über Integrale aufstellen zu können. | auf teilen


m13v0815 In diesem Video geht es um die Ermittlung der Fläche, die zwischen zwei Funktionsgraphen eingeschlossen ist. Dabei sollst du in einer Multiple-Choice-Aufgabe die korrekten Ansätze zur Flächenberechnung auswählen. Es wird gezeigt, dass es mehrere korrekte Möglichkeiten gibt, um dieses Ziel zu erreichen, je nachdem, wie man das Integral aufteilt und Beträge berücksichtigt. Arbeitsblatt zum Download | auf teilen


m13v0827 In dieser Aufgabe sollst du eine Intervallgrenze so berechnen, dass die Flächen, die der Funktionsgraph ober- und unterhalb der x-Achse einschließt, gleich groß sind. Schaffst du es, das mit nur einem einzigen Integral zu berechnen? Arbeitsblatt zum Download | auf teilen


m13v0500 In diesem Video wird eine Steckbriefaufgabe vorgestellt, wobei diesmal auch die Integralrechnung mit ins Spiel kommt, denn eine auszuwertende Eigenschaft der gesuchten Funktion ist die Angabe über eine Fläche, die der Graph der Funktion mit der x-Achse einschließt. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0465 Dies ist eine hilfsmittelfreie Aufgabe zur Integralrechnung, die so ähnlich im Abi des Landes NRW 2019 gestellt wurde. Hier sollen zum einen Schnittstellen zweier Funktionen bestätigt werden und dann die zwischen den Graphen eingeschlossene Fläche bestimmt werden. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0719 In dieser Aufgabe geht es darum, die Funktionsgleichung einer ganzrationalen Funktion mithilfe verschiedener gegebener Eigenschaften zu rekonstruieren. Hierzu müssen die zweite Ableitung der Funktion, ein bestimmter Punkt auf dem Graphen sowie die Steigung der Tangente an einer bestimmten Stelle berücksichtigt werden. Die Lösung dieser Aufgabe erfordert auch den Einsatz der Integralrechnung. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen