Zufallsgrößen


m13v0483 In diesem 1. Lektionsvideo über Zufallsgrößen werden die grundlegenden Begriffe Zufallsgröße/Zufallsvariable und Wahrscheinlichkeitsverteilung erklärt. | auf teilen
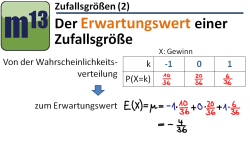

m13v0484 In dieser Lektion lernst du, was man unter dem Erwartungswert einer Zufallsgröße versteht und wie man diesen berechnet. Der Erwartungswert einer Zufallsgröße X gibt an, welcher Wert für X durchschnittlich bei einer großen Zahl von Durchführungen des Zufallsexperimentes zu erwarten ist. | auf teilen


m13v0745 Dies ist eine Übungsaufgabe zur Berechnung des Erwartungswertes einer diskreten Zufallsgröße am Beispiel des Würfelns mit einem fairen Würfel. Arbeitsblatt zum Download | auf teilen


m13v0550 Bei dieser Aufgabe aus der Serie "So ähnlich im Abi gesehen" fehlt die Wahrscheinlichkeit für einen Wert der Zufallsvariable X zur Komplettierung der Wahrscheinlichkeitsverteilung. Wie musst du jetzt vorgehen, um den Erwartungswert E(X) zu bestimmen? Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
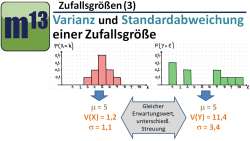

m13v0514 In dieser Lektion geht es über die Streumaße einer Zufallsgröße: Varianz und Standardabweichung. An zwei Verteilungen, die denselben Erwartungswert haben, wird gezeigt, welche Aussage Varianz bzw. Standardabweichung liefern. Es wird gezeigt, wie man Varianz und Standardabweichung berechnet, und warum man das so macht... | auf teilen
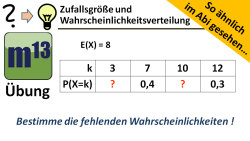

m13v0472 Bei dieser Übung sollst du eine Tabelle zur Wahrscheinlichkeitsverteilung ergänzen, in der zwei Ereigniswahrscheinlichkeiten fehlen. Als weitere Information ist der Erwartungswert angegeben. Dies ist ein Video aus der der Serie "So ähnlich im Abi gesehen". Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0777 Bei diesen Aufgaben nutzt du Wahrscheinlichkeitsverteilungstabellen und den Erwartungswert, um fehlende Werte zu ermitteln und zu überprüfen, ob die Standardabweichung bestimmte Bedingungen erfüllt. Ein guter Test, um dein Verständnis von Verteilungen und statistischen Größen zu vertiefen. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0784 In dieser Aufgabe lernst du, eine Wahrscheinlichkeitsverteilung aus vorgegebenem Erwartungswert und Varianz zu rekonstruieren ? eine umgekehrte Situation, in der du die Wahrscheinlichkeiten berechnest, statt den Erwartungswert oder die Varianz zu ermitteln. Dafür musst du die Formeln für Erwartungswert und Varianz anwenden und geschickt mit den Gleichungen arbeiten, um die gesuchten Wahrscheinlichkeiten zu bestimmen. Arbeitsblatt zum Download | auf teilen
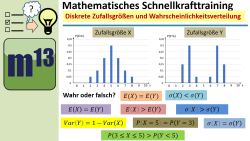

m13v0720 Dies ist eine Übung, mit der du dein Verständnis für die Eigenschaften der Wahrscheinlichkeitsverteilung einer diskreten Zufallsgröße überprüfen kannst, einschließlich des Erwartungswerts, der Standardabweichung und kumulierten Wahrscheinlichkeiten. Arbeitsblatt zum Download | auf teilen


m13v0534 Ein wichtiger Aufgabentyp, der nach Besprechung des Erwartungswertes von Zufallsgrößen behandelt wird, ist die Frage, ob ein Glücksspiel "fair" ist. Ein Glückspiel ist ja ein Zufallsversuch, und von einem fairen Spiel spricht man, wenn der Erwartungswert für Gewinn gleich Null ist - d.h. langfristig würden Anbieter und Kunden das Glücksspiel wohl eher zum Spaß als zum Geldverdienen durchführen. In diesem Video schauen wir uns drei Varianten des Aufgabentyps zum fairen Spiel an: (1) Prüfen, ob ein Glückspiel fair ist; (2) Wie muss man den Einsatz wählen, damit das Spiel fair ist? (3) Wie muss an die Gewinnauszahlung abändern, damit das Glücksspiel fair ist? | auf teilen
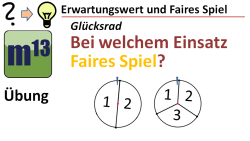

m13v0294 In diesem Video wird ein typischer Aufgabentyp zum "fairen Spiel" vorgestellt Wie groß muss der Einsatz sein, damit das Spiel fair ist? Ein Spiel ist fair, wenn der Erwartungswert des Gewinns (unter Berücksichtigung des Spieleinsatzes) gleich Null ist. Du musst also den Erwartungswert berechnen können, du musst aber auch wissen, wie man die zugrunde liegende Wahrscheinlichkeiten für die möglichen Spielausgänge berechnen kann (Baumdiagramm, Pfad- und Summenregel). In diesem Video wird alles langsam und ausführlich erklärt. Arbeitsblatt zum Download | auf teilen


m13v0716 Bei dieser Aufgabe wird eine Wahrscheinlichkeitsverteilung für ein Glücksspiel untersucht und der Erwartungswert des Gewinns für den Spieler und den Anbieter analysiert. Dabei wird auch gezeigt, wie Änderungen am Einsatz- und Auszahlungsschema den Erwartungswert beeinflussen können. Darüber hinaus sollst du ein Gewinnspiel im Format eines Urnenzieh-Versuchs entwickeln, das zur gegebenen Wahrscheinlichkeitsverteilung passt. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen