Ebenen II (zusätzlich Normalenform und Koordinatenform)
Im Kapitel Ebenen I haben wir ausschließlich die Parametergleichung der Ebene verwendet. Es gibt aber noch weitere Darstellungsmöglichkeiten von Ebenen. In diesem Kapitel Ebenen II kommt jetzt noch die Normalenform und die Koordiantenform der Ebene dazu. Unter anderem wirst du lernen, wie man die verschiedenen Formen ineinander umwandeln kann.Die Ebenengleichung in Normalenform
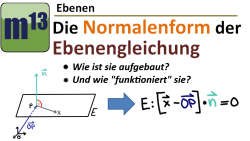

m13v0463 Die Parameterform der Ebenengleichung kennst du ja schon. Hier lernst du eine weitere Form der Ebenengleichung kennen − die sogenannte Normalengleichung. Diese Gleichung beinhaltet zwei Informationen: einen Punkt der Ebene und einen Normalenvektor (dies ist ein Vektor, der senkrecht zur Ebene steht). Wie man diese Zutaten zusammenbringt, und welche Rolle auch noch das Skalarprodukt dabei spielt, das erfährst du in diesem Video. | auf teilen


m13v0462 In diesem Video wird gezeigt, wie man überprüft, ob ein Punkt auf der Ebene liegt (Punktprobe), wenn die Gleichung der Ebene in Normalenform angegeben ist. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
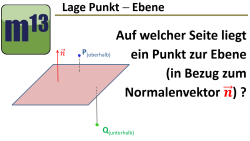

m13v0703 Eine Ebene teilt den dreidimensionalen Raum in zwei Halbräume. In diesem Lektionsvideo lernst du, wie man untersuchen kann, in welchem Halbraum ein außerhalb der Ebene liegender Punkt sich befindet. Als Bezug für die Richtung der Halbräume wird dabei der Normalenvektor der Ebene verwendet, so wie man ihn aus der Ebenengleichung ablesen kann. Arbeitsblatt zum Download | auf teilen
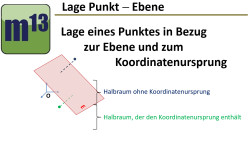

m13v0704 Eine Ebene teilt den dreidimensionalen Raum in zwei Halbräume. Sofern die Ebene selbst nicht durch den Ursprung geht, enthält einer der beiden Halbräume den Koordinatenursprung. In diesem Video wird geprüft, ob ein Punkt des Raumes entweder im Halbraum mit oder ohne Ursprung liegt, oder sogar in der Ebene liegt. Arbeitsblatt zum Download | auf teilen
Die Ebenengleichung in Koordinatenform


m13v0063 In diesem Video wird gezeigt, wie man überprüft ob ein gegebener Punkt auf einer Ebene liegt, die in Koordinatenform angegeben ist. | auf teilen


m13v0389 Gegeben sind eine unvollständige Ebenengleichung in Koordinatenform und drei Ebenenpunkte, von denen auch nicht alle Koordinaten bekannt sind. Die Ebenengleichung und die Punktkoordinaten sind so zu ergänzen, dass die Punkte auf der Ebene liegen. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0558 Bei dieser Aufgabe aus der Serie "So ähnlich im Abi gesehen" soll ein Ausschnitt einer Ebene (die in Koordinatenform gegeben ist) ins dreidimensionale Koordinatensystem gezeichnet werden. Außerdem soll der Flächeninhalt des Dreiecks bestimmt werden, welches durch die Ebene auf einer Koordinatenebene mit den Koordinatenachsen abgegrenzt wird. Arbeitsblatt zum Download | auf teilen


m13v0297 Bei dieser Aufgabe geht es darum, einen geforderten Zusammenhang zwischen Normalenvektor einer Ebene und Ortsvektoren von Ebenenpunkten als Gleichung zu formulieren und diese dann zu lösen. (So ähnlich im Abi gesehen: Bayern 2017, hilfsmittelfreier Teil) Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0512 Bei dieser Aufgabe ist die Koordinatenform einer Ebene gegeben. Nun sucht man den Punkt bzw. die Punktmenge, bei denen alle bzw. zwei Koordinaten übereinstimmen. Eine Aufgabe aus der Reihe "So ähnlich im Abi gesehen". Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0576 Die Gleichung der Ebene E ist in Koordinatenform gegeben. Der Koordinatenursprung O soll an der Ebene E gespiegelt werden, wodurch der Spiegelpunkt O?? entsteht. Außerdem soll die zu Ebene E parallele Ebene F bestimmt werden, die den Punkt O?? enthält. Ein Video aus der Serie "So ähnlich im Abi gesehen". Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0657 Hier sollst du nachweisen, dass es sich bei einer gegebenen Ebenenschar um ein Ebenenbüschel handelt. Die gemeinsame Schnittgerade ist zu bestimmen. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
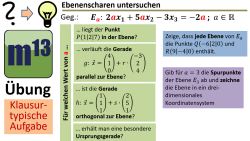

m13v0730 In diesem Video behandeln wir eine typische Klausuraufgabe zu Ebenenscharen, bei der wir verschiedene Aspekte der Lagebeziehungen zwischen einer Geraden und einer Ebene in Abhängigkeit vom Scharparameter untersuchen. Arbeitsblatt zum Download | auf teilen


m13v0671 Bei dieser Aufgabe soll untersucht werden, ob eine gegebene Ebene zu einer Ebenenschar gehört. Arbeitsblatt zum Download | auf teilen
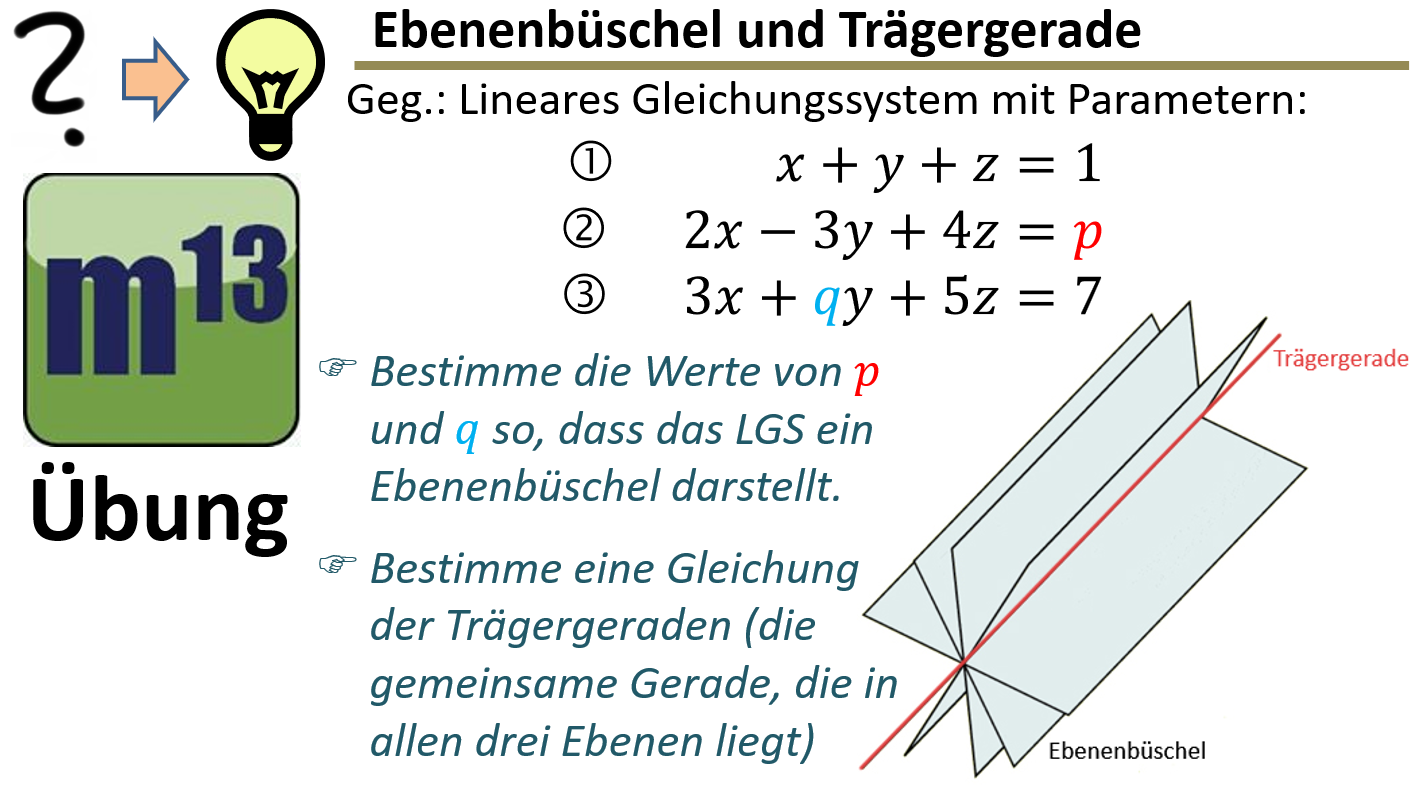

m13v0803 Bestimme die zwei Parameter in einem linearen Gleichungssystem (LGS) so, dass die Gleichungen ein Ebenenbüschel bilden, das sich in einer gemeinsamen Geraden (Trägergerade) schneidet. Anschließend sollst du eine Gleichung dieser Trägergeraden aufstellen. Arbeitsblatt zum Download | auf teilen
Spurpunkte und Spurgeraden einer Ebene

m13v0280 Dieses Video fasst noch einmal zusammen, was Spurpunkte und Spurgeraden sind. Spurpunkte gibt es bei Geraden und Ebenen, Spurgeraden gibt es bei Ebenen. | auf teilen


m13v0167 In diesem Video wird vorgemacht, wie man die Spurpunkte einer Ebene bestimmt, wenn die Ebene in Koordinatenform angegeben ist. | auf teilen

m13v0408 Die Spurgeraden einer Ebene sind die Schnittgeraden der Ebene mit den Koordinatenebenen des Koordiantensystems. In diesem Video wird gezeigt, wie man die Spurgeraden bestimmt, wenn die Ebene in Koordinatenform gegeben ist. | auf teilen


m13v0088 In diesem Video geht es um die Konstruktion einer Ebene, die parallel zu einer gegebenen Ebene liegt und durch einen ebenfalls vorgegebenen Punkt (außerhalb der ersten Ebene geht). In diesem Video werden alle Fälle behandelt, d.h. die vorgegebene Ebene kann in Parameterform, in Normalenform und in Koordinatenform vorliegen... | auf teilen
Konstruktionsmöglichkeiten von Ebenen

m13v0214 Bei dieser Übungsaufgabe soll man eine Ebenengleichung aufstellen; man kennt einen Punkt der Ebene, von dem senkrecht eine Strecke zu einem Punkt außerhalb der Ebene zeigt. Die berechnete Ebene soll dann ins Koordinatensystem eingezeichnet werden. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
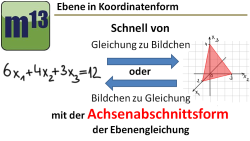

m13v0562 Die Achsenabschnittsform ist eine Darstellungsform einer Ebenengleichung, in der die Schnittstellen der Ebene mit den Koordinatenachsen vorkommen. In diesem Video erfährst du, wie hilfreich diese Form ist, wenn man ein Ebenenbildchen gegeben hat und man eine Gleichung der Ebene aufstellen soll. Auch die Herleitung der Achsenabschnittsform wird besprochen. | auf teilen
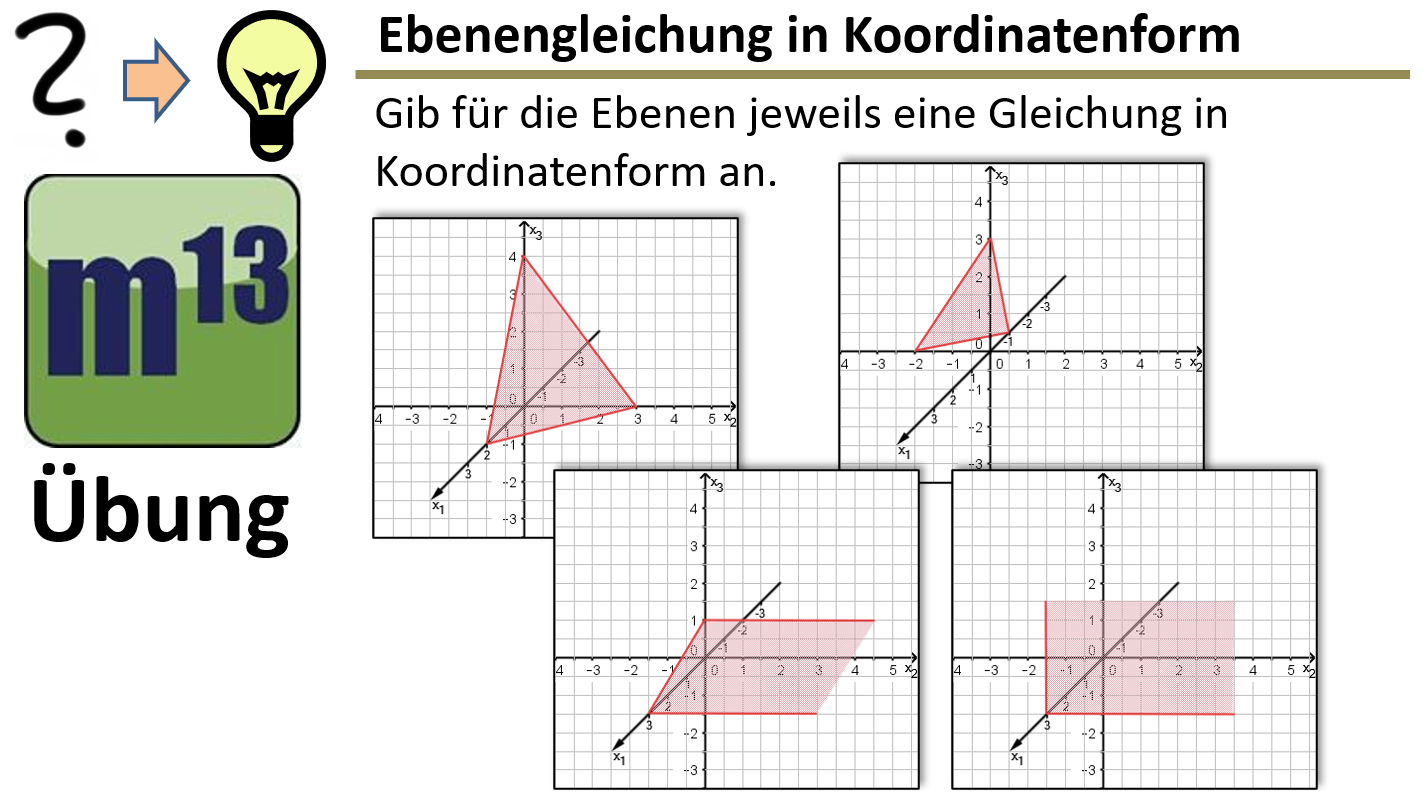

m13v0855 In dieser Aufgabe sollst du aus einer Schrägbild-Darstellung die Koordinatengleichung einer Ebene bestimmen. Besonders hilfreich ist dabei die Achsenabschnittsform, mit der sich Ebenen direkt aus ihren Schnittpunkten mit den Koordinatenachsen aufstellen lassen. Zudem lernst du, wie man mit Ebenen in besonderer Lage umgeht, die parallel zu Achsen verlaufen oder einzelne Achsen nicht schneiden. Arbeitsblatt zum Download | auf teilen
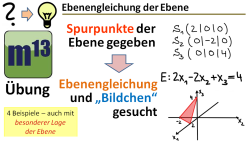

m13v0561 Wenn man die Spurpunkte einer Ebene (also die Schnittpunkte mit den Koordinatenachsen) kennt, dann ist es ein Leichtes, daraus eine Koordinatengleichung der Ebene zu entwickeln, wenn man die Achsenabschnittsform kennt. Umgekehrt ist es auch nicht schwer, aus der Koordinatenform der Ebene, die Achsenabschnittsform aufzustellen, aus der man dann die Spurpunkte ganz leicht ablesen kann. In diesem Übungsvideo wird beides vorgemacht. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0089 In diesem Video geht es um die Konstruktion einer Ebene, die spiegelsymmetrisch zu zwei gegebenen Punkten liegt. Die Ebene wird in Normalen- bzw. Koordinatenform berechnet, da dies hier der bequemste Weg ist. | auf teilen
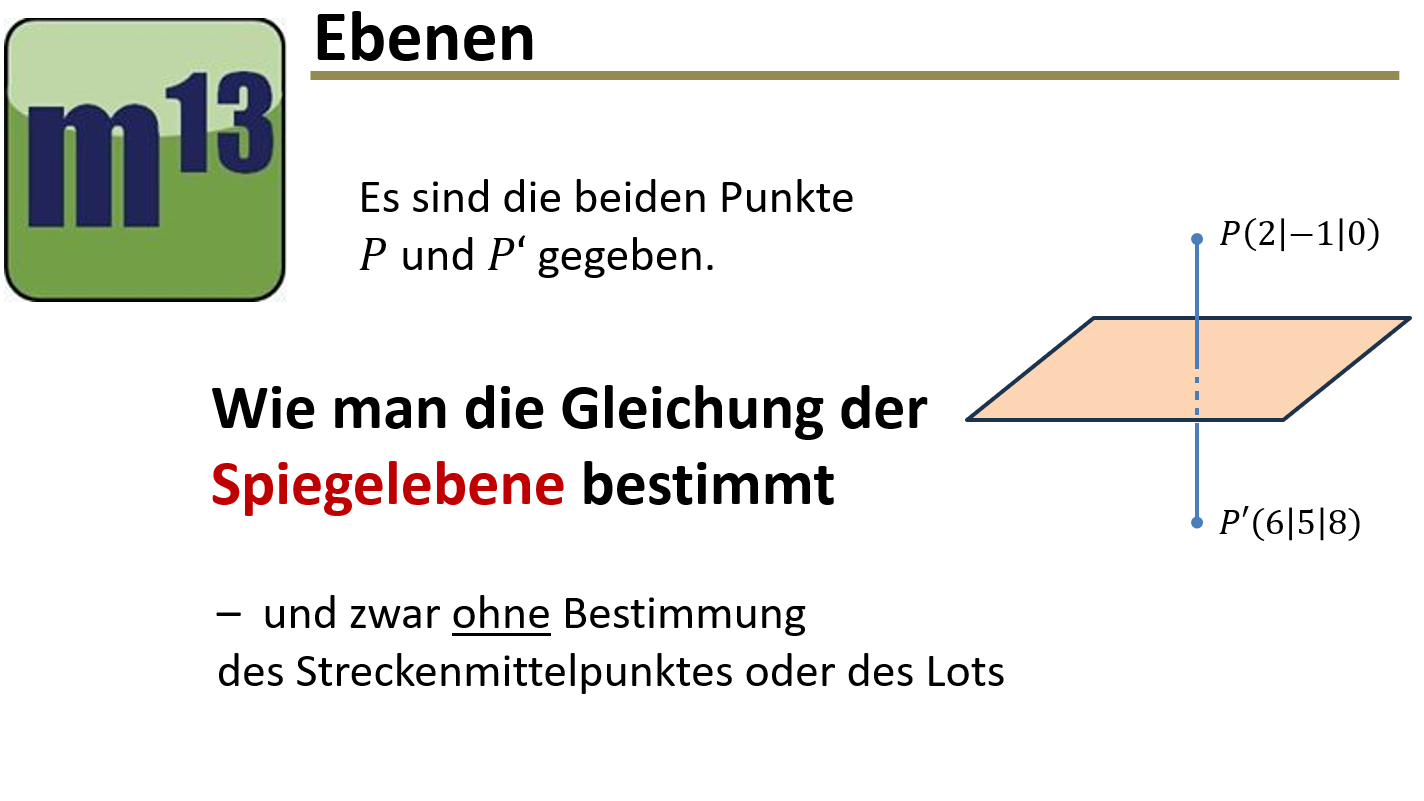

m13v0824 In diesem Video wird eine Methode zur Bestimmung der Spiegelebene zwischen zwei Punkten vorgestellt, die - im Gegensatz zur Methode im Video m13v0089 - ohne die Berechnung des Mittelpunktes und der Lotrichtung auskommt. Arbeitsblatt zum Download | auf teilen


m13v0832 In dieser Aufgabe sollst du Punkte auf den Koordinatenachsen finden, die von zwei gegebenen Punkten gleich weit entfernt sind. Dabei nutzt du zwei verschiedene Lösungswege: die Abstandsformel und eine Hilfsebene, die zwischen den Punkten liegt. Die Aufgabe fordert strategisches Denken und verbindet wichtige Konzepte aus der Vektorrechnung und analytischen Geometrie. Arbeitsblatt zum Download | auf teilen
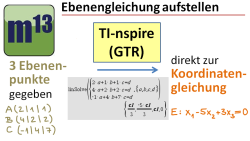

m13v0286 Wie man aus drei gegebenen Punkten (die natürlich nicht auf einer Geraden liegen dürfen) durch das Aufstellen eines LGS direkt zur Koordinatenform der Ebene kommt wird in diesem Video vorgemacht. Dies ist eine schnelle Methode, wenn man den GTR hierfür einsetzen darf. | auf teilen
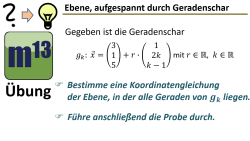

m13v0698 Gegeben ist eine Geradenschar, wobei alle Geraden der Schar in einer Ebene liegen. Hier sollst du eine Koordinatengleichung der dieser Ebene bestimmen. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
Ebenengleichungen ineinander umwandeln
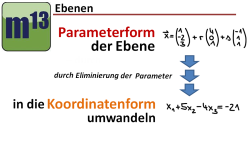

m13v0486 In diesem Video lernst du eine weite Methode zur Umwandlung einer Parametergleichung einer Ebene in die Koordinatenform kennen - per Eliminierung der Parameter mittels eines Verfahrens, das dem Gauß-Verfahren ähnelt. | auf teilen
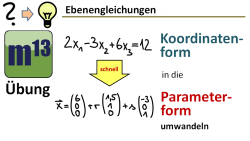

m13v0565 In einem früheren Video (m13v0004)hatten wir eine Methode kennengelernt, mit der man die Koordinatenform der Ebenengleichung in die Parameterform überführen kann. In diesem Video lernst du eine andere Methode kennen, die vielleicht noch schneller geht. | auf teilen


m13v0439 Bei dieser Aufgabe geht es um die Darstellung einer Ebene in Parameterform und Koordinatenform. Es ist eine Koordinatenform gegeben, und du sollst entscheiden, welche der vier angegebenen Parametergleichungen eine Beschreibung der Ebene ist, welche in Koordinatenform vorgegeben ist (dabei kann es mehrere richtige Möglichkeiten geben). Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
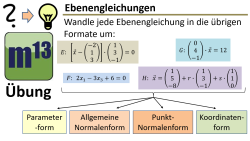

m13v0700 In diesem Übungsvideo geht es um das Umformen von Ebenengleichungen zwischen den verschiedenen Formaten, also: Parameterform, allgemeine Normalenform, Punkt-Normalenform und Koordinatenform. Jede angegebene Form soll in die anderen Formen umgewandelt werden. Arbeitsblatt zum Download | auf teilen


m13v0424 Eine Übungsaufgabe zur Umwandlung zwischen Normalen- und Koordinatenform einer Ebene. Dabei sollen vorgegebene Gleichungen mit Parametern so angepasst werden, dass diese dieselbe Ebene beschreiben. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
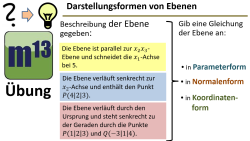

m13v0689 Die Beschreibung einer Ebene ist gegeben. Jetzt sollst du diese Ebene in Parameterform, Normalenform und Koordinatenform angeben. Arbeitsblatt zum Download | auf teilen


m13v0470 Bei dieser Übung hast du Kärtchen mit Ebenengleichungen bzw. mit Beschreibungen von besonderen Ebenenlagen gegeben, und du sollst passende Kärtchen zuordnen. Dabei geht es darum, dass zu weißt, wie man Parameterform, Normalenform und Koordinatenform ineinander umwandelt und wie man an der Ebenengleichung eine besondere Lage der Ebene im Koordinatensystem erkennen kann. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
Besondere Lage von Ebenen schnell erkennen
Gegenseitige Lage Ebene-Ebene


m13v0107 In diesem Video wird erklärt, wie man die gegenseitige Lage zweier Ebenen untersucht, wenn diese beide in Koordinatenform gegeben sind, und wie man - sofern vorhanden - die Schnittgerade bestimmt. | auf teilen


m13v0108 In diesem Video wird erklärt, wie man die gegenseitige Lage zweier Ebenen untersucht, wenn eine in Parameterform, die andere in Koordinatenform gegeben ist, und wie man - sofern vorhanden - die Schnittgerade bestimmt. | auf teilen
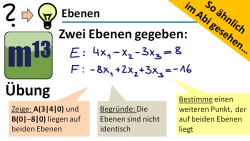

m13v0440 Eine mehrteilige Übungsaufgabe zu Ebenen, die in Koordinatenform angegeben sind. Es geht um Punktproben, gegenseitige Lage von Ebenen. Diese hilfsmittelfreie Aufgabe ist eine typische Aufgabe aus dem Bereich der Analytischen Geometrie, wie sie in Klausuren (oder im Abi) gestellt werden könnte. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0608 Bei dieser Aufgabe aus der Serie "So ähnlich in Abi gesehen" geht es um die zeichnerische Darstellung zweier Ebenen und ihrer Schnittgeraden im Koordinatensystem. Außerdem soll die Gleichung der Schnittgerade auch rechnerisch bestätigt werden. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0735 Diese Transferaufgabe erfordert das Zusammenführen von Kenntnissen über die Lagebeziehung von Ebenen und die Lösungsmenge von linearen Gleichungssystemen. Eine typische Aufgabe für den hilfsmittelfreien Teil in der Klausur. Arbeitsblatt zum Download | auf teilen
Gegenseitige Lage von Ebenen und Geraden


m13v0015 In diesem Video zeige ich, wie man die gegenseitige Lage einer Geraden und einer Ebene bestimmt, wenn die Gerade in Parameterform und die Ebene in Koordinatenform gegeben ist. | auf teilen


m13v0694 Kannst du aus den angegebenen Bedingungen zu Stütz-, Richtungs- und Normalenvektoren ergründen, welche (besondere) Lage zwischen Gerade und Ebene vorliegt? Arbeitsblatt zum Download | auf teilen


m13v0213 Eine Übungsaufgabe zum Thema Ebenen und Geraden: Eine Gerade ist gegeben, und man soll alle Ebenen bestimmen, die parallel zu dieser Geraden liegen. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0380 In diesem Video geht es um die Bestimmung des Schnittpunktes einer Gerade und einer Ebene (in Koordinatenform gegeben). Außerdem soll geprüft werden, ob die Gerade die Ebene senkrecht schneidet. Ein weiteres Video aus der Serie "So ähnlich im Abi gesehen"; eine ähnlich Aufgabe wurde im hilfsmittelfreien Teil im Abi des Landes NRW im Jahr 2017 gestellt. Arbeitsblatt zum Download | auf teilen


m13v0670 Eine Aufgabe zur Lagebeziehung Gerade − Ebene: zunächst Parallelität einer Gerade zur Ebene nachweisen und dann die Gerade an der Ebene spiegeln. Arbeitsblatt zum Download | auf teilen


m13v0545 Bei diesem Video aus der Serie "So ähnlich im Abi gesehen" soll gezeigt werden, dass sich zwei Geraden senkrecht schneiden und der Schnittpunkt soll angegeben werden. Schneidende Geraden definieren natürlich eine Ebene; diese soll in Koordinatenform angegeben werden. Bei dieser Aufgabe kann man (mit dem notwendigen Background-Wissen) vieles ohne Rechnung bestimmen ? von daher vielleicht eine interessante, hilfsmittelfreie Aufgabe. Arbeitsblatt zum Download | auf teilen


m13v0733 Eine Ebene und eine Gerade können sich in verschiedenen räumlichen Anordnungen zueinander befinden. In dieser Aufgabe soll untersucht werden, welche Lagebeziehungen zwischen einer Ebene und den Geraden einer Geradenschar möglich sind. Arbeitsblatt zum Download | auf teilen
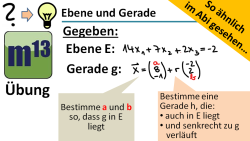

m13v0492 Bei diesen Aufgaben aus der Serie "So ähnlich im Abi gesehen" geht es um das Wechselspiel zwischen Ebene (angegeben in Koordinatenform) und Gerade. Zu einen soll die Parametergleichung der Geraden g so ergänzt werden, dass diese in der angegebenen Ebene liegt; zum zweiten soll man dann eine weitere Gerade bestimmen, die ebenfalls in der Ebene liegt und die senkrecht zur Geraden g liegt. Arbeitsblatt zum Download | auf teilen


m13v0547 Bei diesem Video aus der Serie "So ähnlich im Abi gesehen" geht es um den rechnerischen Nachweis der senkrechten Ausrichtung einer Gerade zu einer Ebene, welche in Koordinatenform angegeben ist; auch der Schnittpunkt ist zu bestimmen. Außerdem sollst du zeigen, dass du die Methode der graphischen Vektoraddition verstehst, mit der weitere Punkte zu ermitteln sind. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0794 Bei dieser Aufgabe sollst du die Gleichung einer Geraden aufstellen, die gegebene Eigenschaften erfüllt. Sie soll orthogonal zu einer gegebenen Ebene stehen und die y-Achse in einem Punkt schneiden, der einen bestimmten Abstand zu einem weiteren angegebenen Punkt hat. Damit ist dies eine komplexe Aufgabe, die mit mehreren Kompetenzen bedient werden muss. Arbeitsblatt zum Download | auf teilen
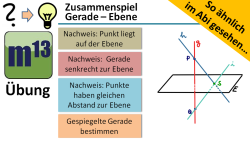

m13v0554 Ein weiteres Video aus der Serie "So ähnlich im Abi gesehen". Hier geht es im Wesentlichen (1.) um das Aufstellen einer Gerade, die durch zwei Punkte geht; (2.) um den Nachweis, dass diese Gerade senkrecht zu einer Ebene (gegeben in Koordinatenform) steht; (3) um das Aufstellen der Gleichung einer Geraden, die durch Spiegelung einer anderen Geraden an einer Ebene entsteht. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0610 Bei dieser Aufgabe soll zunächst die gegenseitige Lage zwischen Gerade und Ebene (in Koordinatenform) untersucht werden. Danach soll die Gerade an der Ebene gespiegelt werden und eine Gleichung der gespiegelten Gerade ermittelt werden. Ein Video aus der Serie "So ähnlich im Abi gesehen". Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen





