Ebenen I
Nach den Geraden kommen die Ebenen. Im dreidimensionalen Raum gibt es - anders als bei den Geraden - mehr als nur die Parameterdarstellung. In manchen Grundkursen wird nur die Parameterdarstellung der Ebene behandelt; aus diesem Grund wird das Kapitel unterteilt in Ebenen I und Ebenen II. Ebenen I behandelt nur die Parameterdarstellung der Ebene, im Kapitel Ebenen II werden dann zusätzlich die Normalenform und die Koordinatenform der Ebene besprochen.Die Ebenengleichung in Parameterform


m13v0050 In diesem Einstiegsvideo wird erklärt, wie die vektorielle Darstellung einer Ebene in Raum funktioniert. Die Begriffe Stützvektor und Spannvektor werden erklärt. Du solltest am Ende verstehen, dass jeder Punkt der Ebene durch zwei Parameterwerte eindeutig bestimmt ist. | auf teilen


m13v0062 In diesem Video wird gezeigt, wie man überprüft, ob ein gegebener Punkt auf einer Ebene liegt, die in Parameterform gegeben ist. Diese sogenannte Punktprobe ist ein sehr wichtiger Aufgabentyp, der fast garantiert in der ersten Klausur über Ebenen vorkommt. Hier muss man ein lineares Gleichungssystem lösen. | auf teilen
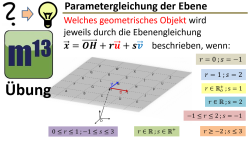

m13v0702 Mit der Parametergleichung der Ebene lassen sich durch bestimmte Einschränkungen der Parameterwerte verschiedene geometrische Objekte darstellen. In diesem Übungsvideo sollst du ermitteln, welche Objekte in Abhängigkeit der Vorgaben zu den Parametern beschrieben werden. Arbeitsblatt zum Download | auf teilen
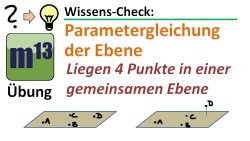

m13v0262 Eine Abwandlung der Frage, ob ein Punkt auf einer Ebene liegt, ist die Frage, ob vier Punkte auf einer Ebene liegen. Erkennst du, warum das praktisch dieselbe Frage ist? Wiederum ist dies ein beliebter Aufgabentyp. Arbeitsblatt zum Download | auf teilen


m13v0065 Eine Ebene ist eindeutig durch drei Punkte definiert (man kann eine Platte auf drei Punkten ablegen, ohne dass es irgendwo wackelt, wobei die Punkte allerdings nicht auf einer Geraden liegen dürfen). Wie man aus drei gegebenen Punkten eine Ebenengleichung in Parameterform aufstellen kann, lernst du in diesem Video. Du wirst auch lernen, dass es mehrere Möglichkeiten gibt, eine Ebenengleichung aufzustellen. Eine klausurtypische Aufgabe. | auf teilen


m13v0165 In diesem Video wird vorgemacht, wie man die Spurpunkte einer Ebene bestimmt, wenn die Ebene in Parameterform angegeben ist. Spurpunkte sind die Schnittpunkte einer Ebene mit den Koordinatenachsen. | auf teilen


m13v0737 Bei dieser Aufgabe hast du zwei Spurgeraden einer Ebene gegeben und du sollst die dritte Spurgerade bestimmen. Im Video werden zwei Lösungsmöglichkeiten behandelt. Arbeitsblatt zum Download | auf teilen
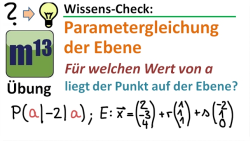

m13v0263 Eine Abwandlung der Punktprobe: ein Punkt mit einem oder zwei Parametern a ist angegeben. Man soll den Wert von a so bestimmen, dass der Punkt auf der Ebene liegt. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
Weitere Konstruktionsm


m13v0066 Eine Gerade und ein Punkt abseits dieser Geraden legt eindeutig die Lage einer Ebene im Raum fest. In diesem Video wird gezeigt, wie man bei gegebener Gerade und Punkt daraus die Ebenengleichung in Parameterform herleitet. | auf teilen


m13v0067 Zwei parallele Geraden legen eindeutig die Lage einer Ebene im Raum fest. Hier lernst du, wie man die zugehörige Ebenengleichung in Parameterform daraus ermittelt. | auf teilen


m13v0068 Eine Ebene ist eindeutig bestimmt durch zwei sich schneidende Geraden. Die Geraden bilden dann ja so eine Art "Kreuz" auf die man die Ebene ablegen kann. In diesem Video lernst du, wie man aus den gegebenen Geradengleichungen zweier sich schneidender Geraden, die Parametergleichung der dadurch definierten Ebene aufstellen kann. | auf teilen
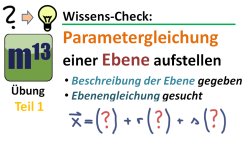

m13v0230 In diesem Übungsvideo kannst du prüfen, ob du eine Parametergleichung einer Ebene aufstellen kannst, wenn die Konstruktionsweise der Ebene angegeben ist. Dies ist ein häufiger Aufgabentyp, der meistens dann in Klausuren abgefragt wird, wenn ihr gerade mit Ebenen im Unterricht angefangen habt und die Parameterdarstellung der Ebene als erstes kennengelernt habt. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
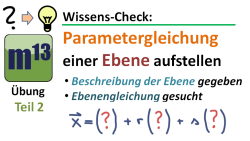

m13v0231 Teil 2 der Übungsaufgabe. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0678 Eine weitere Konstruktionsaufgabe für Ebenen: zwei Punkte der Ebene sind gegeben, und man weiß, dass die Ebene parallel zur z-Achse ist. Arbeitsblatt zum Download | auf teilen
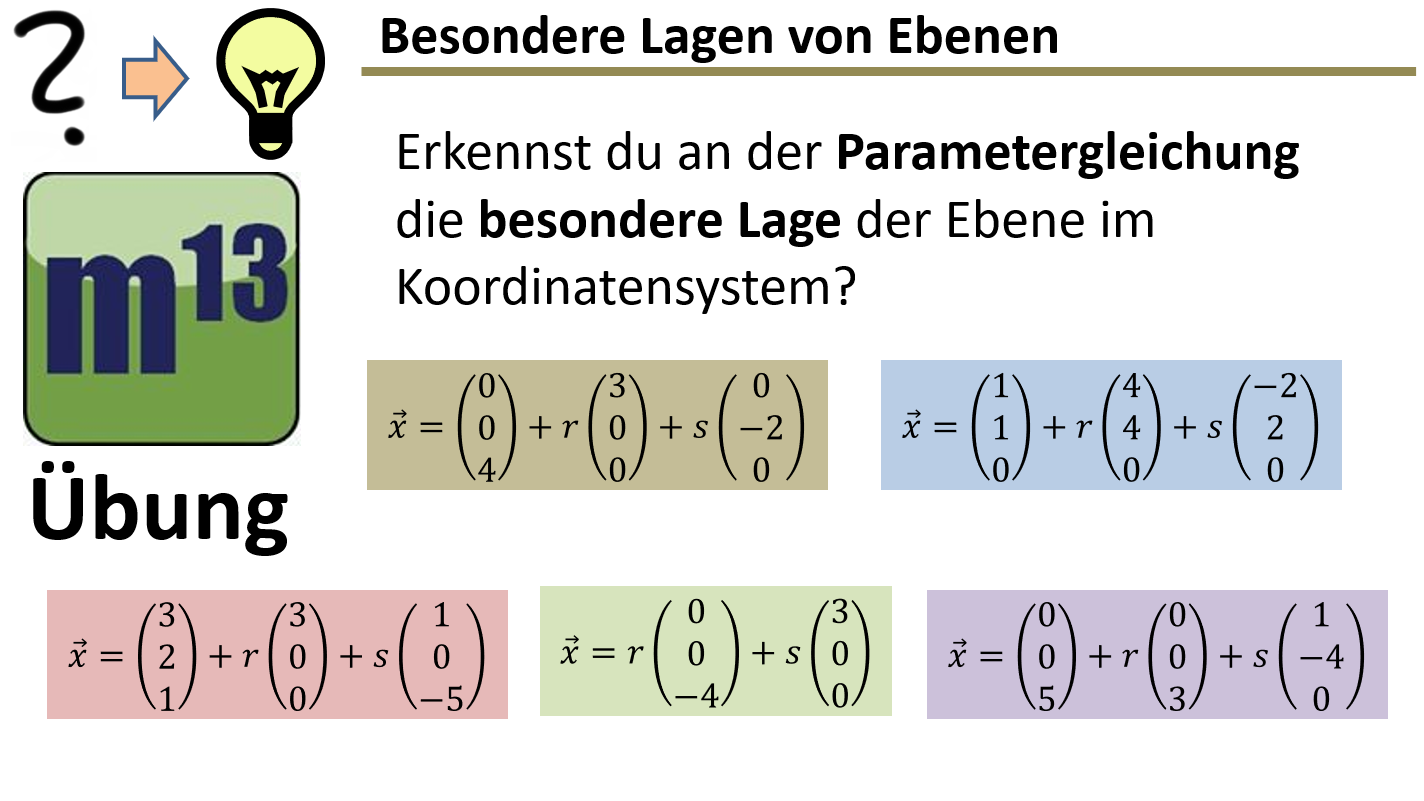

m13v0850 Mit dieser Aufgabe kannst du überprüfen, ob du die Funktionsweise der Parametergleichung einer Ebene verstanden hast. Ziel ist es, aus der Ebenengleichung abzuleiten, ob die Ebene eine besondere Lage im Koordinatensystem hat - zum Beispiel ob sie parallel oder identisch zu einer Koordinatenebene ist oder eine Koordinatenachse enthält. Arbeitsblatt zum Download | auf teilen
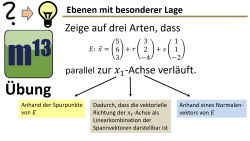

m13v0669 Eine Aufgabe zur Vernetzung deines Wissens: Hier geht es darum, dass du auf verschiedene Arten die besondere Lage einer Ebene (die in Parameterform gegeben ist) nachweist. Arbeitsblatt zum Download | auf teilen
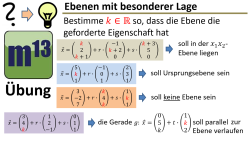

m13v0690 Dies ist eine anspruchsvolle Aufgabe, bei der du den Scharparameter einer Ebenenschar so bestimmen sollst, dass eine Ebene mit der geforderten (besonderen) Lage entsteht. Hierzu musst du wissen, durch welche Eigenschaften der Stütz- und Richtungsvektoren eine besondere Lage entsteht... Arbeitsblatt zum Download | auf teilen


m13v0691 In diesem Video schauen wir auf Geradenscharen, bei denen der Scharparameter nur im Richtungsvektor vorkommt. Da der Stützvektor für alle Geraden der Schar gleich ist, gehen die Geraden alle durch den zugehörigen Stützpunkt. Im Video wird erklärt, warum alle Geraden der Schar in einer gemeinsamen Ebene liegen und wie man eine Gleichung dieser Ebene ermittelt. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0692 In diesem zweiten Video betrachten wir Geradenscharen, bei denen der Scharparameter nur im Stützvektor vorkommt. Da der Richtungsvektor für alle Geraden der Schar gleich ist, sind die Geraden alle parallel und liegen daher in einer Ebene. Es wird beschrieben, wie man eine Gleichung dieser gemeinsamen Ebene ermittelt. Arbeitsblatt zum Download | auf teilen
Dreieck und Parallelogramm als spezielle Ausschnitte von Ebenen
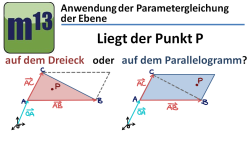

m13v0335 Die Spannvektoren einer Ebene spannen ein Dreieck bzw. ein Parallelogramm auf. In diesem Video wird gezeigt, wie man die Parametergleichung einer Ebene nutzen kann, um zu prüfen, ob ein Punkt innerhalb oder außerhalb eines Dreiecks bzw. Parallelogramms liegt. | auf teilen
Ebenen (in Parameterform) und Geraden im Zusammenspiel


m13v0016 In diesem Video wird vorgemacht, wie man die gegenseitige Lage einer Gerade und einer Ebene untersucht, wenn sowohl Gerade als auch Ebene in Parameterform angegeben sind. Es gibt drei Möglichkeiten: (1.) die Gerade scheidet die Ebene - dann kann man auch den Schnittpunkt berechnen; (2.) die Gerade verläuft parallel zur Ebene; und (3.) die Gerade verläuft in der Ebene. | auf teilen


m13v0409 Bei dieser Übungsaufgabe ist ein Lösungsweg zur Untersuchung der gegenseitigen Lage von Gerade und Ebene beschrieben - allerdings ohne Kommentare. Du sollst nun kommentieren, was gemacht wurde, und warum... Arbeitsblatt zum Download | auf teilen


m13v0349 Bei dieser Übungsaufgabe ist ein Lösungsweg zur Untersuchung der gegenseitigen Lage von Gerade und Ebene beschrieben - allerdings ohne Kommentare. Du sollst nun kommentieren, was gemacht wurde, und warum... Arbeitsblatt zum Download | auf teilen


m13v0366 In diesem Video geht es darum, wie man (1.) ohne Punktprobe untersuchen kann, ob drei Punkte auf einer Geraden liegen; (2.) das Aufstellen einer Ebenengleichung aus drei Punkten; (3.) die Anwendung des Kriteriums für rechte Winkel (Orthogonalität) bei Vektoren. Dies ist ein Video aus der Reihe "So ähnlich im Abi gesehen". Eine ähnliche Aufgabe wurde im Abi des Landes NRW 2017 im hilfsmittelfreien Teil gestellt. Arbeitsblatt zum Download | auf teilen
