Differentialrechnung II
Weitere Ableitungsregeln
In der Einführungsphase hast du die grundlegenden Ableitungsregeln kennengelernt, die du bei Funktionen anwenden kannst, die in Potenzschreibweise geschrieben werden können. Im Folgenden lernst du weitere Ableitungsregeln kennen, mit denen zusammengesetzte Funktionen abgeleitet werden können (verkettete Funktionen, Produkte und Quotienten von Funktionen). Außerdem wirst du die besondere Eigenschaft der e-Funktion beim Ableiten kennenlernen.
Bevor wir über die Kettenregel als weitere wichtige Ableitungsregel sprechen können, müssen wir uns vorher noch klar machen, was verkettete Funktionen eigentlich sind. Dies wird in den nachfolgenden Videos behandelt.
m13v0031 In diesem Video wird die Kettenregel zum Ableiten von verketteten Funktionen ausführlich erklärt. | auf teilen
m13v0032 In diesem Video wird die Produktregel zum Ableiten ausführlich erklärt. Die Produktregel kommt zum Einsatz, wenn man sich die abzuleitende Funktion als Produkt zweier Funktionen vorstellen kann: f(x) = u(x)·v(x) | auf teilen
m13v0033 In diesem Video wird die Quotientenregel zum Ableiten ausführlich erklärt. Die Quotientenregel kommt zum Einsatz, wenn man sich die abzuleitende Funktion als Quotient zweier Funktionen vorstellen kann: f(x) = u(x)/v(x) | auf teilen
m13v0843 In diesem Video leitest du die erweiterte Produktregel für die Ableitung einer Funktion mit drei Faktoren her. Dabei zeigst du nicht nur die allgemeine Formel, sondern auch, wie sich die Ableitung in eine alternative Darstellung mit logarithmischer Differentiation umformen lässt. | Arbeitsblatt zum Download | auf teilen
m13v0845 Bei dieser Aufgabe sollst du dir die allgemeine Formel zur Ableitung mehrfach-verketteter Funktionen selbst erarbeiten. Voraussetzung dafür ist, dass du die Verkettungsstruktur der Funktion analysierst und die Kettenregel systematisch bis zum Schluss anwendest. | Arbeitsblatt zum Download | auf teilen
m13v0428 Ein Video aus der Serie "So ähnlich im Abi gesehen ", diesmal zur Ableitung von etwas komplexeren Funktionen. Diese enthalten trigonometrische Funktionen. Ähnliche Aufgaben wurden im Abi des Landes Baden-Württemberg im hilfsmittelfreien Teil gestellt. | Arbeitsblatt zum Download | auf teilen
m13v0429 Dies ist der zweite Teil der Miniserie "Ableiten wie im Abi". Die Ableitung solcher Funktionen solltest du im Abi ohne Probleme bewältigen können. Bei diesen Aufgaben kommen e-Funktionen als Faktoren vor, und du solltest schnell erkennen können, wann die Kettenregel und wann die Produktregel anzuwenden ist... | Arbeitsblatt zum Download | auf teilen
m13v0731 Bei dieser Aufgabe sollst du mithilfe deiner Kenntnisse allgemeiner Ableitungsregeln selbst eine Regel für die Ableitung einer speziellen Funktion herleiten: die Ableitung einer reziproken Funktion. Im Anschluss sollst du diese Regel für eine Beispielfunktion anwenden. | Arbeitsblatt zum Download | auf teilen
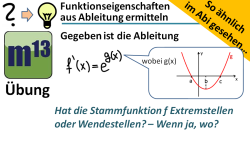
m13v0493 Dies ist eine interessante Aufgabe über das Zusammenspiel zwischen einer Exponentialfunktion mit innerer Funktion, und außerdem über das Zusammenspiel von dieser verketteten Funktion und ihren Ableitungen. Welche Schlussfolgerungen lassen sich bezüglich Extrem- und Wendestellen ziehen? Eine ähnliche Aufgabe kam im hilfsmittelfreien Teil einer Abiturklausur dran. | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
m13v0556 Bei dieser Aufgabe aus der Serie "So ähnlich im Abi gesehen" geht es um die sichere Anwendung von Untersuchungsmethoden der Funktionsanalyse. Zum einen sollen Extremstellen nachgewiesen werden; in einer weiteren Aufgabe soll gezeigt werden, dass es für die gegebene Funktion nur einen Berührpunkt mit der x-Achse gibt. | Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
m13v0328 Kommst du drauf, wie man die Funktion f(x)=x hoch x ableitet? - Man braucht einen kleinen Trick... Im Video siehst du, wie es geht. | Arbeitsblatt zum Download | auf teilen
Steckbriefaufgaben
Bei einer sogenannten Steckbriefaufgabe wird eine Funktion anhand charakteristischer Eigenschaften (Funktionstyp, Extrem-, Wendepunkte, Nullstellen, Steigungsverhalten etc.) beschrieben, und man soll damit den Funktionsterm der Funktion bestimmen. Dazu werden die angegebenen besonderen Eigenschaften in eine Reihe von Funktionsgleichungen übersetzt, die zunächst noch Unbekannte enthalten. Durch Lösen eines Linearen Gleichungssystem werden diese Unbekannten ermittelt und so letztlich die gesuchte Funktionsgleichung gefunden. Die ersten beiden Videos sind Grundlagenvideos; später kommen noch weitere Beispiele hinzu.
m13v0255 In diesem Video lernst du, wie man allgemein an sogenannte Steckbriefaufgaben herangeht. Alternativ spricht spricht man bei diesem Aufgabentyp auch von Rekonstruktion oder Modellierung von Funktionen mit vorgegebenen Eigenschaften. Die allgemeine Herangehensweise wird an einem Beispiel erklärt, bei dem eine ganzrationale Funktion dritten Grades gesucht wird. | auf teilen
m13v0256 In diesem zweiten Video wird vorgemacht, wie du bei Steckbriefaufgaben die angegebenen Funktionseigenschaften in Bedingungen und Gleichungen übersetzt. Dies ist der wichtigste und oft schwierigste Part bei Steckbriefaufgaben. Mit Hilfe der aufgestellten Gleichungen werden anschließend die Funktionsparameter bestimmt. | Arbeitsblatt zum Download | auf teilen
m13v0398 Dies ist eine typische Steckbriefaufgabe zur Ermittlung einer ganzrationalen Funktion. | Arbeitsblatt zum Download | auf teilen
m13v0400 Eine weitere Übungsaufgabe zur Rekonstruktion einer ganzrationalen Funktion. | Arbeitsblatt zum Download | auf teilen
m13v0467 Eine weitere Steckbriefaufgabe, bei der der Funktionsterm einer ganzrationalen Funktion dritten Grades gesucht wird. Achsenschnittpunkt, Wendepunkt und eine Eigenschaft der Wendetangente sind gegeben. | Arbeitsblatt zum Download | auf teilen
m13v0699 Eine weitere Steckbriefaufgabe: Gesucht ist eine quadratische Funktion. Diese Aufgabe aus der Serie "So ähnlich im Abi gesehen" ist interessant, weil sie nicht eine der "Standard-Steckbriefaufgaben" ist, weil die mathematische Formulierung der Funktionseigenschaften hier etwas anspruchsvoller ist. | Arbeitsblatt zum Download | auf teilen
m13v0798 Diese Aufgabe zeigt, dass nicht jede Steckbriefaufgabe, die mit Standardverfahren gelöst werden kann, zu einer Funktionsgleichung führt, die den Anfangsbedingungen entspricht. Es ist daher ratsam, den Graphen der erstellten Funktion zu plotten und mit den Vorgaben abzugleichen. Auch die Gründe, warum solche Probleme auftreten können, werden besprochen. | Arbeitsblatt zum Download | auf teilen
m13v0705 Eine weitere Steckbriefaufgabe. Interessant ist, dass hier Eigenschaften von zwei Funktionen und ihr "Zusammenspiel" ausgewertet werden müssen, um die Gleichung der gesuchten Funktion zu bestimmen. | Arbeitsblatt zum Download | auf teilen
m13v0806 Dies ist eine anspruchsvollere Steckbriefaufgabe für eine ganzrationale Funktion dritten Grades, da aus den geforderten Funktionseigenschaften mehrere Bedingungen herausgelesen werden müssen, um die erforderliche Anzahl an Gleichungen für das lineare Gleichungssystem zu ermitteln. | Arbeitsblatt zum Download | auf teilen
m13v0729 Bei dieser Aufgabe soll man die Funktionsgleichung für eine quadratische Funktion ermitteln. Hierzu sind der Scheitelpunkt und einen weiteren Punkt auf dem Funktionsgraphen gegeben. Die Aufgabe besteht darin, sie auf zwei unterschiedliche Arten zu lösen und anschließend den Aufwand zu vergleichen: einmal mithilfe der Differenzialrechnung und einmal unter Verwendung der Scheitelpunktform. | Arbeitsblatt zum Download | auf teilen
Extremwertaufgaben
Zu den wichtigsten Anwendungsaufgaben der Differentialrechnung zählen die sogenannten Extremwertaufgaben. Hierbei gilt es im Anwendungskontext zu untersuchen, wann eine Zielgröße maximal oder minimal (oder allgemein: extremal) wird. Es gibt verschiedene Arten von Extremwertaufgaben. Allen gemein ist, dass man zuerst eine Zielfunktion aufstellen muss - manchmal mit, manchmal ohne Nebenbedingung. Wenn man die Zielfunktion in Abhängigkeit einer Variablen aufgestellt hat, untersucht man diese mit den Mitteln der Differentialrechnung und Analysis auf relative bzw. absolute Extrema. Hier werden verschiedene - oft typische - Extremwertaufgaben präsentiert.
m13v0186 Dies ist ein klassisches Einstiegsbeispiel für Extremwertaufgaben. Die Zielfunktion hängt zunächst von zwei Variablen ab, und man benötigt eine Nebenbedingung, um daraus eine Zielfunktion zu machen, die nur von einer Variablen abhängt. Hier wird ausführlich erklärt, aus welchen Schritten die Lösungsstrategie einer Extremwertaufgabe besteht. | auf teilen
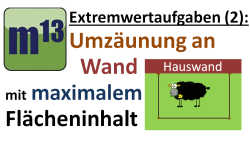
m13v0187 Eine weitere Extremwertaufgabe mit Nebenbedingung. Ein rechteckiges Gehege, das an einer Hauswand errichtet wird, soll maximalen Flächeninhalt haben. Dafür stehen 60 Meter Maschendrahtzaun zur Verfügung. | auf teilen
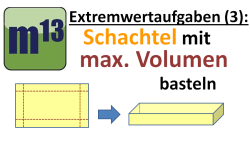
m13v0188 Eine weitere Extremwertaufgabe, diesmal ohne Nebenbedingung. Man soll aus einem rechteckigen Stück Pappe eine Schachtel basteln, die ein möglichst großes Fassungsvermögen hat. | auf teilen
m13v0189 Eine weitere Extremwertaufgabe: Hier soll man eine Konservendose mit 800 ml Inhalt so designen, dass die Oberfläche (also der Blechverbrauch) minimal wird. | auf teilen
m13v0190 Eine weitere Extremwertaufgabe, diesmal wieder ohne Nebenbedingung. Ein Reckeck soll so zwischen x-Achse und einer nach unten geöffneten Parabel eingepasst werden, dass der Flächeninhalt des Rechtecks maximal wird. | auf teilen
m13v0194 Ein wichtiger Aspekt von Extremwertaufgaben, der leider oft übersehen wird: In diesem Video wird erklärt, warum man bei Extremwertaufgaben auch die Randwerte des Definitionsbereichs prüfen muss. Hier können die "wahren Extremwerte" lauern. Zunächst die theoretische Erklärung, dann folgt ein Beispiel. | auf teilen
m13v0326 Wieder mal eine Fläche eines Vierecks, die sich aufgrund eines Eckpunktes, der über eine Kurve wandert verändert. In diesem Fall setzt sich die Fläche aus zwei Teilflächen zusammen. In diesem Video werden alle Rechenschritte ausführlich behandelt. In dem nächsten Video wird gezeigt, wie man die Aufgabe mit den Hilfsmitteln des GTRs ganz schnell auch lösen kann. | auf teilen
m13v0451 Dies ist ein weiteres Übungsvideo zu Extremwertaufgaben: Mit einem Draht der Länge 36 cm soll eine quaderförmige Säule mit quadratischer Grundfläche konstruiert werden. Dies ist ein Beispiel für eine Extremwertaufgabe mit Nebenbedingung - in diesem Fall ist die Gesamtkantenkänge des Quaders geben. | Arbeitsblatt zum Download | auf teilen
m13v0552 Bei dieser Aufgabe aus der Serie "So ähnlich im Abi gesehen" geht es um eine Extremwertaufgabe, bei dem ein Dreieck mit maximaler Fläche gesucht wird, welches unter dem Graphen einer zusammengesetzten e-Funktion eingeschrieben ist. Das Dreieck hat seine Eckpunkte zum einen im Koordinatenursprung, dann irgendwo auf der positiven x-Achse und an der entsprechenden Stelle auf dem Funktionsgraphen. | Arbeitsblatt zum Download | auf teilen