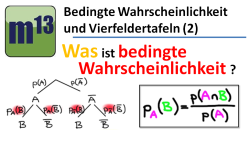
Bedingte Wahrscheinlichkeit und Vierfeldertafel
Du weißt jetzt schon wie man mehrstufige Zufallsexperimente mit Hilfe eines Baumdiagramms veranschaulichen kann. In diesem Abschnitt werden wir uns insbesondere solche Zufallsexperimente anschauen, bei denen die Wahrscheinlichkeit für das zweite Ereignis vom Ausgang der auf der vorhergehenden Stufe abhängt. In diesem Zusammenhang wirst du die wichtigen Begriffe bedingte Wahrscheinlichkeit und totale Wahrscheinlichkeit kennenlernen. Und - last but not least - wirst du erfahren, wie man ein Baumdiagramm in eine sogenannte Vierfeldertafel übertragen kann. Die Vierfeldertafel ist ein nützliches Tool, mit dem sich Berechnungen von Schnittwahrscheinlichkeiten, totale Wahrscheinlichkeiten und bedingte Wahrscheinlichkeiten sehr übersichtlich durchführen lassen.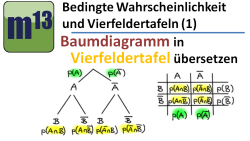

m13v0223 In diesem Video lernst du, wie man ein zweistufiges Baumdiagramm in eine Vierfeldertafel übersetzt. | auf teilen
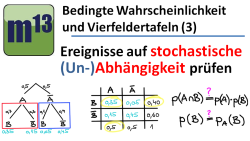

m13v0226 Hier lernst du, was man unter stochastischer Abhängigkeit bzw. stochastischer Unabhängigkeit versteht und prüfen kann, ob zwei Ereignisse stochastisch (un-)abhängig sind. Dies wird zum Schluss an zwei Aufgabenbeispielen erläutert. | auf teilen
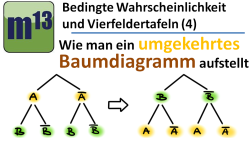

m13v0227 In diesem Video lernst du, wie man ein Baumdiagramm umdrehen kann. Ein verknüftes Zufallsereignis hat oft eine gewisse logische Reihenfolge, mit der man das Zustandekommen dieses verknüpften Ereignisses betrachten kann. Doch manchmal ist es interessant, das Zustandekommen eines Zufallsereignisses von der anderen Seite her zu betrachten. Hier erfährst du, wie das geht, wie man das Umdrehen des Baumdiagramms mit Hilfe der Vierfeldertafel oder über die bedingte Wahrscheinlichkeit berechnen kann und wozu das alles gut ist. Achtung: Im Video gibt es einen kleinen Fehler bei der Beschriftung des Baumdiagramms, siehe dazu einen →Korrekturhinweis. | auf teilen
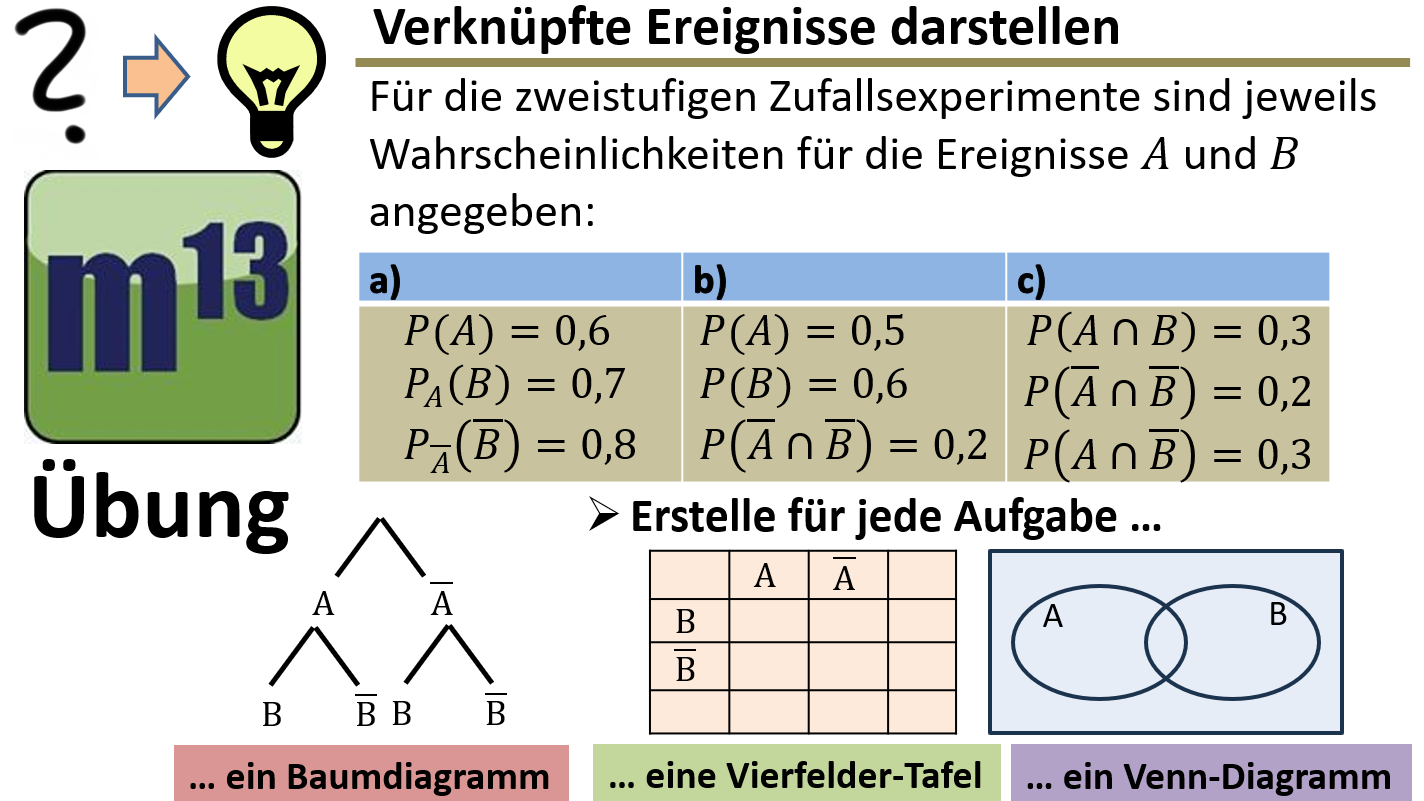

m13v0813 In dieser Aufgabe geht es um die Darstellung und Analyse zweistufiger Zufallsexperimente mit gegebenen Wahrscheinlichkeiten. Deine Aufgabe besteht darin, ein Baumdiagramm, eine Vierfeldertafel und ein Venn-Diagramm zu erstellen. Arbeitsblatt zum Download | auf teilen
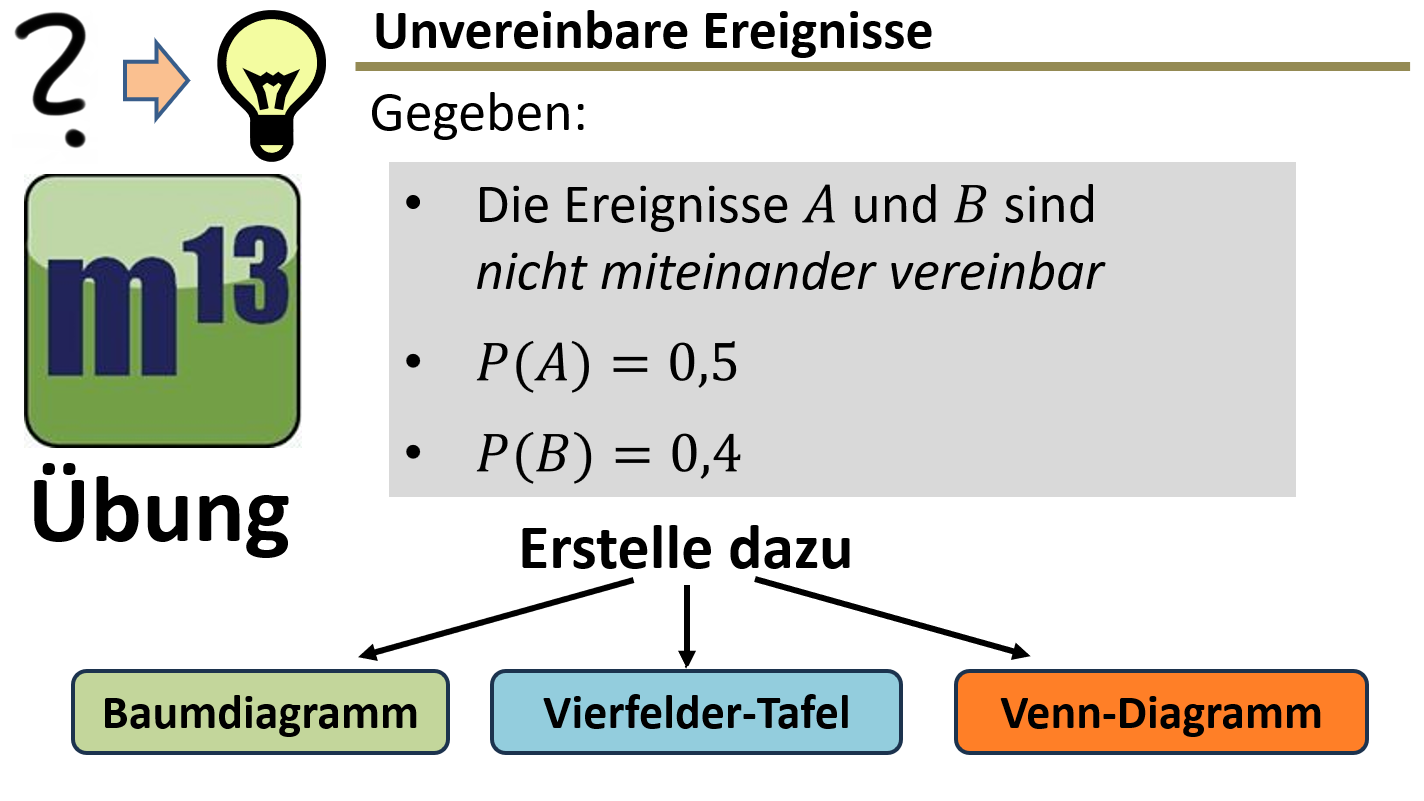

m13v0800 In dieser Aufgabe lernst du, die Zusammenhänge zwischen Baumdiagrammen, Vierfeldertafeln und Venn-Diagrammen zu verstehen und anzuwenden. Du betrachtest dabei den besonderen Fall, dass die Ereignisse A und B nicht miteinander vereinbar sind, und siehst, wie sich dies in den verschiedenen Darstellungsformen widerspiegelt. Arbeitsblatt zum Download | auf teilen
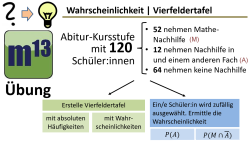

m13v0673 Erstelle mithilfe der Angaben eine Vierfeldertafel mit absoluten Häufigkeiten und Wahrscheinlichkeiten. Darauf aufbauend sollen dann Ereigniswahrscheinlichkeiten ermittelt werden. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
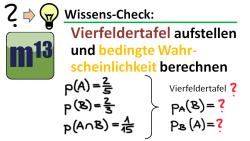

m13v0225 Dies ist eine Übungsaufgabe. Es gilt aus gegebenen Angaben eine Vierfeldertafel zu erstellen und bedingte Wahrscheinlichkeiten zu berechnen. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0774 Nachdem du für ein zweistufiges Zufallsexperiment eine vollständige Vierfeldertafel erstellt hast, sollst du Wahrscheinlichkeiten für bestimmte Ereignisse bestimmen. Dabei lernst du, wie man UND- bzw. ODER-Wahrscheinlichkeiten identifiziert und erkennst, wann die Betrachtung der Gegenwahrscheinlichkeit der schnellere Weg zum Ziel ist. Arbeitsblatt zum Download | auf teilen

m13v0372 In dieser Übungsaufgabe geht es um das Aufstellen einer Vierfeldertafel und um das Rechnen mit totalen Wahrscheinlichkeiten, Schnittwahrscheinlichkeiten und bedingten Wahrscheinlichkeiten. Dies ist ein Video aus der Reihe ?So ähnlich im Abi gesehen?. Eine ähnliche Aufgabe kam im Abitur in Bayern im Jahr 2018 im hilfsmittelfreien Teil dran. Arbeitsblatt zum Download | auf teilen

m13v0228 In dieser Übungsaufgabe sollen bedingte Wahrscheinlichkeiten berechnet werden. Es wird zweimal gewürfelt und es werden die Ereignisse A: "Beim ersten Wurf wird eine Primzahl gewürfelt" und B: "Die Augensumme beträgt mindestens 10" betrachtet. Arbeitsblatt zum Download | auf teilen

m13v0284 In diesem Übungsvideo wird anhand eines Münzwurf-Experiments untersucht, ob zwei Ereignisse stochastisch abhängig oder unabhängig sind. Diese Aufgabe ist vom Anspruch höher im Vergleich zu ähnlichen Aufgaben, bei denen eine Vierfeldertafel gegeben ist, denn hier muss man die Wahrscheinlichkeiten der Ereignisse zunächst berechnen. Arbeitsblatt zum Download | auf teilen
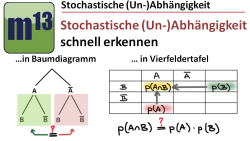

m13v0285 In diesem Video erfährst du, wie man bei gegebenem Baumdiagramm oder Vierfeldertafel sehr schnell erkennen kann, ob die beiden Ereignisse A und B stochastisch abhängig oder unabhängig sind. | auf teilen
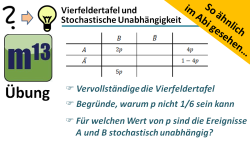

m13v0600 Bei dieser Aufgabe aus der Serie "So ähnlich in Abi gesehen" geht es darum, (1.) eine Vierfeldertafel aufzustellen bzw. zu komplettieren, in der eine variable Wahrscheinlichkeit p auftritt. (2.) solltest du begründen können, warum p hier nicht jeden Wert zwischen 0 und 1 haben kann, und (3.) solltest du wissen, wie man einen Berechnungsansatz für p aufstellt, so dass die Ereignisse A und B stochastisch unabhängig sind. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0793 In diesem Video geht es um die Überprüfung stochastischer Unabhängigkeit bei Ereignissen beim Würfeln. Konkret werden die Ereignisse "Augenzahl größer als 2", "Augenzahl ist eine Primzahl" und "Augenzahl ist gerade" betrachtet. Du sollst analysieren, ob diese Ereignisse unabhängig voneinander sind, indem du ihre Schnittwahrscheinlichkeiten mit den Produkten ihrer Einzelwahrscheinlichkeiten vergleichst. Arbeitsblatt zum Download | auf teilen


m13v0320 Bei dieser Aufgabe soll das umgekehrte Baumdiagramm aufgestellt werden; dazu muss man u.a. die totale Wahrscheinlichkeiten für ein Ereignis bestimmen. Dies ist ein Video aus der Reihe "So ähnlich im Abi gesehen". Eine ähnliche Aufgabe wurde im Abi des Landes Bayern 2016 im hilfsmittelfreien Teil gestellt. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
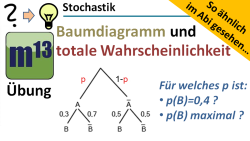

m13v0371 Bei dieser Übungsaufgabe geht es um das Rechnen mit Pfadwahrscheinlichkeiten und der totalen Wahrscheinlichkeit in einem Baumdiagramm. Dies ist ein Video aus der Reihe ?So ähnlich im Abi gesehen?. Eine ähnliche Aufgabe wurde im Abitur in Bayern im Jahr 2018 im hilfsmittelfreien Teil gestellt. Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen
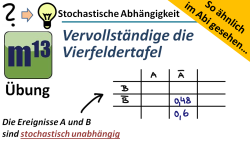

m13v0438 Bei dieser Übungsaufgabe hast du eine teilweise ausgefüllte Vierfeldertafel zu einem zweistufigen Zufallsexperiment gegeben, welche du vervollständigen sollst. Du hast zusätzlich die Information, dass die beiden Ereignisse stochastisch unabhängig sind. Dies ist eine hilfsmittelfreie Aufgabe aus der Serie "So ähnlich im Abi gesehen". Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0491 In dieser Aufgabe wird ein Zufallsexperiment in Form eines Gewinnspiels betrachtet. Ein Glücksrad wird zweimal gedreht; zum einen soll man eine Wahrscheinlichkeitsverteilung für das Gewinnspiel aufstellen, zum zweiten werden zwei Ereignisse betrachtet, welche man auf stochastische Unabhängigkeit überprüfen soll. Dies ist eine Aufgabe aus der Videoserie "So ähnlich im Abi gesehen". Arbeitsblatt zum Download | auf teilen


m13v0606 Krankheit und Schnelltest: Ein Aufgabenklassiker, bei dem es um das Aufstellen eines Baumdiagramms und die Berechnung von Schnittwahrscheinlichkeiten, bedingten Wahrscheinlichkeiten oder totale Wahrscheinlichkeiten geht. Ein weiteres Video aus der Serie "So ähnlich im Abi gesehen". Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen


m13v0607 Bei dieser Aufgabe geht es u.a. um den Satz von Bayes, der angewendet wird, wenn man die umgekehrte bedingte Wahrscheinlichkeit von einer Kombination von Merkmalen berechnen möchte. Wieder mal geht es um den klassischen Sachzusammenhang "Krankheit und Schnelltest"... Ein Video aus der Serie "So ähnlich im Abi gesehen". Arbeitsblatt zum Download | Musterlösung auf Patreon | auf teilen